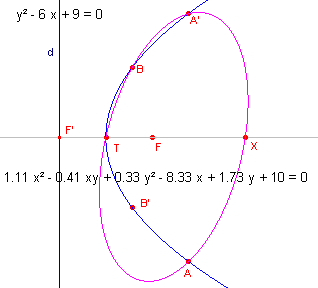Van ellips naar parabool

Uitleg | Download ][ Pooltransformaties | Anal.meetkunde | Cabri-FAQ | Meetkunde | Cabri

Uitleg terug
E�n van de functies in Cabri is "Herdefinieer object", waarmee het oa. mogelijk is een punt opnieuw te defini�ren als snijpunt van twee evenwijdige lijnen.
Hiermee kunnen we illustreren, dat een parabool raakt aan de oneigenlijke rechte.
Zie hiervoor ook Cabri-FAQ: Vraag 10.

We geven twee methodes:

Methode 1 - uitgaande van een parabool
Methode 2 - uitgaande van een ellips met daaraan een raaklijn

Methode 1 terug
We bekijken de onderstaande figuren.

figuur 1 ellipspar1.gif (2339 bytes) In deze figuur is een parabool bepaald door de punten T, A, A', B, B', op basis van het brandpunt F en de richtlijn d.
De constructiestappen zijn als volgt:
1 - Loodlijn(F, d); 2 - Snijpunt(1, d) = F '
3 - Midden(F, F ') = T
4 - PuntOpObject(d) = H 5 - Loodlijn(H, d)
6 - Middelloodlijn(F, H) 7 - Snijpunt(5, 6) = A
8 - Spiegeling(A, 1) = A'
9 - Snijpunt(6, d) = K 10 - Loodlijn(K, 6)
11 - Lijn(A, F);  12 - Snijpunt(10, 11) = B;
13 - Spiegeling(B, d) = B'
14 - Kegelsnede(A', B, T, B', A)

Cabri "herkent" de kegelsnede als een parabool (zie de tekst "Deze parabool" in figuur 1).

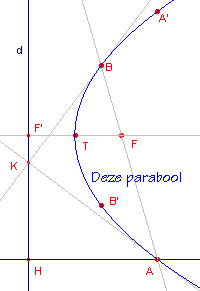
figuur 2 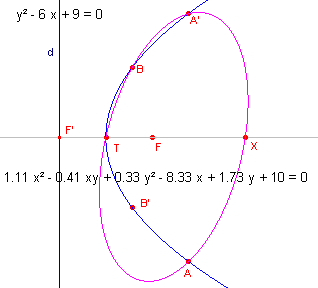ellipspar2.gif (2756 bytes) We kiezen nu op de lijn FF' (de symmetrie-as van de parabool) een willekeurig punt X.
De punten X, A', B, T en A bepalen nu een (andere) kegelsnede.
Kiezen we X op het verlengde van F'F dan is die kegelsnede een ellips.

In figuur 2 zijn ook de vergelijkingen van de parabool en de ellips zichtbaar gemaakt (ten opzichte van een niet-zichtbaar assenstelsel).
figuur 3

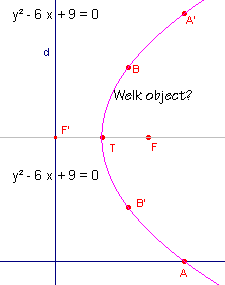
ellipspar3.gif (1865 bytes)

 We kiezen nu de functie "Herdefini�erObject" en defini�ren het punt X als snijpunt van de symmetrie-as en de lijn door A evenwijdig daaraan.

Het gevolg staat in figuur 3.
We zien dat de vergelijking van de ellips nu gelijk is aan de vergelijking van de parabool.
Ook aan de tekst "Welk object" is te zien, dat er nu twee objecten getekend zijn.
Van de ellips is slechts ��n punt terecht gekomen op de oneigenlijke rechte.
Een parabool is "dus" een ellips waarvan ��n punt op de oneigenlijke rechte ligt.

Methode 2 terug
Opmerking. In onderstaande figuren is gebruik gemaakt van de Cabri macro:Ellips4P1r.mac.

figuur 4 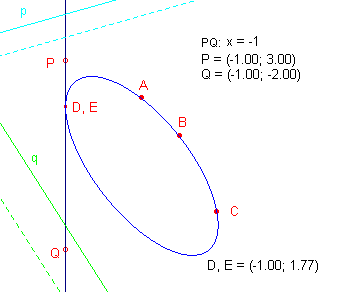ellipspar4.gif (4521 bytes) Zie figuur 4.
Hierbij gaan we uit van ellips bepaald door de punten A, B, C, D, E, waarbij D en E samenvallen. In D is de raaklijn PQ aan de ellips getekend.
De punten P en Q zijn onafhankelijke punten. Het punt D,E is een willekeurig punt van PQ.
We zullen de punten P en Q door herdefinitie laten samenvallen met opvolgend het �oneigenlijk punt � van een (willekeurige) lijn pen het  � oneigenlijke punt � van een (willkeurige) lijn q.
Beide oneigenlijke punten zijn voor Cabri het "snijpunt" van de lijn p en een lijn daarmee evenwijdig en het "snijpunt" van de lijn q en een lijn daarmee evenwijdig.
Nb.
Zie ook de vergelijking van PQ en de co�rdinaten van de punten P, Q en D.
figuur 5 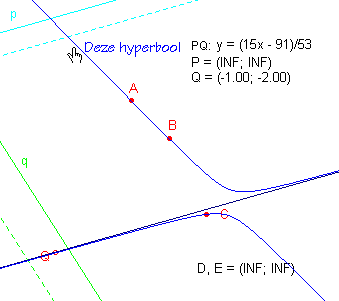ellipspar5.gif (4497 bytes) Zie figuur 5.
Via de Cabri-functie "Herdefinieer object" is allereerst het punt P "verplaatst" naar het oneindige.
Zie daarvoor de co�rdinaten van P: (INF; INF) en D,E: (INF; INF).
De ellips verandert daardoor in een hyperbool.
Nb.
De lijn PQ is nu evenwijdig met de lijn p (PQ is een asymptoot van de hyperbool).
figuur 6 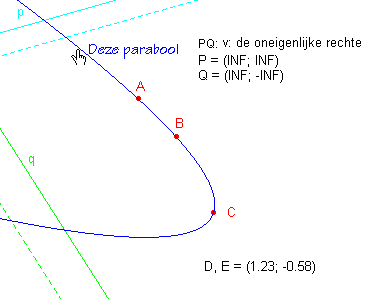ellipspar6.gif (4201 bytes) In figuur 6 is ook het punt Q verplaatst naar het oneindige.
De lijn PQ is nu overgegaan in de � oneigenlijke recht �.
De co�rdinaten van Q zijn naar verwacht: (INF; INF).
Nb.
Vermoedelijk door een interne fout in Cabri zijn de co�rdinaten van D, E echter weer re�el.

Opmerking
Klik hier voor een behandeling van de kegelsneden op basis van Pooltransformaties.
Op die pagina komt het begrip � oneigenlijke rechte � ook aan de orde.
[einde Opmerking]

Download terug
De figuren op deze pagina kunnen NIET MEER worden gedownload. In het bestand is tevens de macro:Ellips4P1r.mac opgenomen.
 

begin pagina
[ellips-parab.htm] laatste wijziging op: 19-01-18