Cabri-werkblad
Overzicht ][
Alle werkbladen | Meetkunde | Cabri
Overzicht -
Co�rdinaten in Cabri 
Inleiding
Als je een nieuw Cabri-tekenblad kiest, dan gebeurt er op de
achtergrond al heel wat, waarvan we (gelukkig?) niets zien.
E�n van die dingen is, dat Cabri (in eerste instantie voor eigen gebruik) een
assenstelsel cre�ert.
Teken je nu bijvoorbeeld een punt op het tekenblad, dan voegt Cabri daaraan direct (en
vooralsnog onzichtbaar) de co�rdinaten toe.
Maar, we kunnen die co�rdinaten zichtbaar maken en er ook mee werken.
We zullen zien dat Cabri vergelijkingen van lijnen kan bepalen en grafieken van functies
kan tekenen.
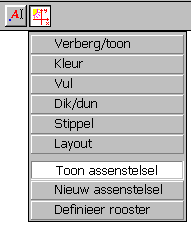
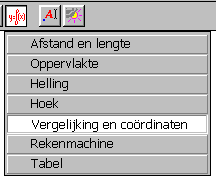
De Cabri-functies die hierbij gebruikt worden, bevinden zich in twee menu’s: in het Layout-menu
("Toon assenstelsel") en in het Reken-menu ("Vergelijking en
co�rdinaten"); zie figuur 1.
| figuur 1 |
 |
|
 |
|
Layout-menu |
|
Reken-menu |
Opdracht 1
Kies dus maar een nieuw tekenblad en teken daarop
een punt P.
Ga naar het Layout-menu en kies de functie "Toon
assenstelsel"; kies vervolgens in het Reken-menu de functie "Vergelijking
en co�rdinaten".
Selecteer nu het reeds getekende punt P.
Je ziet dan iets als:
| figuur 2 |
 |
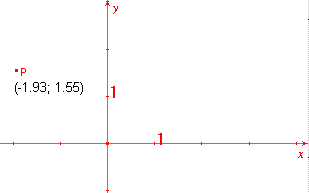De co�rdinaten van P hangen af van het
zichtbare assenstelsel.
Opmerking
Het feit, dat de co�rdinaten in figuur 2 in twee decimalen worden
weergeven, is afhankelijk van de (door je docent) gekozen instellingen.
[einde Opmerking] |
Verplaats nu de oorsprong van het assenstelsel
en kijk wat er met de co�rdinaten van P gebeurt.
Verplaats ook het punt P.
Kijk eens wat er gebeurt als je het punt op de x-as
dat met een 1
is aangegeven (Deze eenheid), naar rechts of
naar links verplaatst. Geef een korte beschrijving.
Opdracht 2
Teken op hetzelfde tekenblad nu ook een punt Q.
Teken de lijn door P en Q.
Kies nu in het Reken-menu weer "Vergelijking en
co�rdinaten" en selecteer dan de lijn PQ.
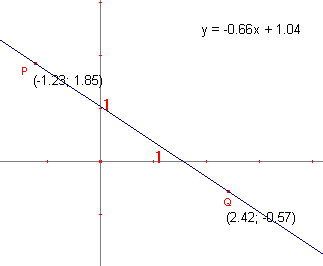
Cabri bepaalt nu dus de vergelijking van de lijn ten opzichte van
het weergegeven assenstelsel (zie figuur 3a).
| figuur
3a |
|
figuur 3b |
 |
|
 |
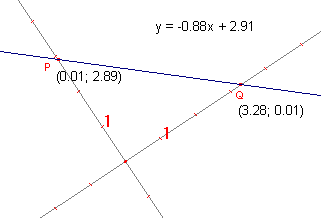- Verplaats nu het punt Q zo, dat PQ loodrecht staat op de y-as.
- Kan je aan de vergelijking zien, dat er inderdaad sprake is
van loodrechte stand? Verklaar je antwoord.
- Verplaats nu het punt P zo, dat PQ loodrecht staat op de x-as.
- Kan je aan de vergelijking zien, dat er sprake is van
loodrechte stand? Verklaar je antwoord.
- Verplaats nu de oorsprong horizontaal en/of verticaal.
- Welke waarde in de vergelijking van de lijn blijft nu
onveranderd? Waarom is dat?
- Selecteer nu de x-as (Deze assen), houd je linker
muisknop ingedrukt en draai de as in tegenwijzerrichting (zie figuur 3b).
- Verklaar nu waarom beide getallen in de vergelijking van de
lijn PQ veranderen.
Een macro
In het Layout-menu staat nog een functie die we kunnen
gebruiken als we met een assenstelsel werken: "Definieer rooster" (zie
figuur 4a).
figuur 4a |
|
figuur 4b |
 |
|
 |
Layout -menu |
|
Constructie -menu |
Opdracht 3
Alleen als je een assenstelsel hebt gekozen (gedaan met
"Toon assenstelsel"), kan je de functie "Definieer rooster" gebruiken.
Kies de functie "Definieer rooster" en
selecteer daarna (klik op) �en van de assen van het assenstelsel (Deze assen).
Alle punten met gehele co�rdinaten worden nu op het
tekenblad zichtbaar. Dit zijn dus de roosterpunten.
- Kies in het Punt-menu de functie "Punt".
- Beweeg dan de Wijzer over het tekenblad. Wat merk je op, als je met
de Wijzer in de buurt van een roosterpunt komt?
- Teken het punt met co�rdinaten (3 ; 1).
Het is niet mogelijk op deze manier het punt met co�rdinaten (3� ;
1�) te tekenen. Immers dat is geen roosterpunt.
We zullen voor deze toepassing een macro ontwerpen.
- Kies een nieuw tekenblad en maak het assenstelsel zichtbaar
("Toon assenstelsel").
- Gebruik de functie "Wijzig getallen" in het Extra-menu
om twee getallen (voor de x- en y-co�rdinaat van het te tekenen punt) op
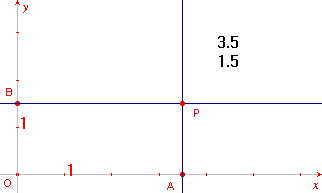
het tekenblad te zetten (zie figuur 5: de getallen 3.5 en 1.5).
| figuur 5 |
 |
Aanwijzing
Na het kiezen van de functie moet je ergens op het tekenblad klikken; dan opent zich een
speciaal venstertje, 
, waarin je "drie punt
vijf" typt.
Daarna klik je op een andere plaats op het tekenblad en je typt "1.5" in
eenzelfde venstertje.
[einde Aanwijzing]
We leggen nu de x-co�rdinaat op de x-as vast met de
functie "Maat overbrengen" uit het Constructie-menu (zie
figuur 4b).
- Kies deze functie, selecteer het getal 3.5 en klik daarna op de x-as.
Op de x-as staat nu een punt (A in figuur 5) op de positie 3,5.
- Doe hetzelfde met het getal 1.5 (zie het punt B in
figuur 5).
- Teken nu een loodlijn door A op de x-as, en een loodlijn door
B op de y-as.
Het snijpunt van beide loodlijnen is het punt P.
Je kan nu de macro:PuntCoord vastleggen.
- Kies in het Macro-menu de functie "Beginobjecten".
- Selecteer het getal 3.5 (Dit getal), dan het getal 1.5 en tenslotte �en van de
assen (Deze assen).
- Kies in het Macro-menu de functie "Eindobjecten".
- Selecteer het punt P.
- Kies in het Macro-menu de functie "Definieer macro".
- Bewaar de macro op disk (aangeven bij "Opslaan in
bestand").
Opmerking
We zullen deze macro in Opdracht 4 gebruiken.
[einde Opmerking
Grafieken
De methode die hierboven is weergegeven, kunnen we, enigszins
gewijzigd, ook gebruiken om grafieken van functies te tekenen.
Kortweg gezegd:
een functie is een voorschrift waarmee bij een (willekeurige)
waarde van x de bijbehorende waarde van y wordt vastgelegd.
De "meetkundige plaats" van alle punten (x,
y) is dan de grafiek van de functie.
Opdracht 4
We willen nu de grafiek tekenen van y = �x2
+ 1/x.
- Kies een nieuw tekenblad met daarop het assenstelsel. Zorg ervoor,
dat de macro:PuntCoord beschikbaar is.
Kies nu een willekeurig punt X op de x-as (met
"Punt op object"; Op deze as).
Toon de co�rdinaten van dat punt (met de functie "Vergelijking
en co�rdinaten").
De x-waarde van het punt X gebruiken we om met de
"Rekenmachine" (zie ook het Cabri-werkblad
"Rekenmachine") de bijbehorende y-waarde te bepalen.
- Voer de bedoelde berekening met Cabri’s Rekenmachine uit (zie
figuur 6).
| figuur 6 |
 |
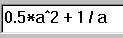Opmerking
Selecteer telkens als de waarde van x nodig is, de x-co�rdinaat van het punt X, die
door Cabri geplaatst is in de variabele a.
[einde Opmerking] |
De y-waarde zetten we, na het klikken op de knop [=] van de
Rekenmachine, op het tekenblad (klik op de uitkomst en dan op de gewenste positie op het
tekenblad).
Kies nu de macro:PuntCoord; deze staat onderaan in het Macro-menu.
Selecteer de x-co�rdinaat van het punt X (Dit getal), selecteer dan het
getal achter "Resultaat:" en klik tot slot op �en van de assen.
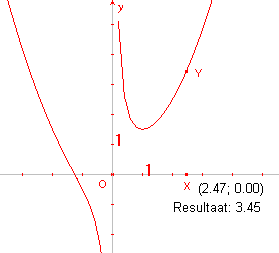
Het punt met co�rdinaten (x, y) wordt dan op het
tekenblad geplaatst (zie punt Y in figuur 7).
| figuur 7 |
 |
Kies dan de functie "Meetkundige
plaats" in het Constructie-menu.
- Selecteer het punt Y en vervolgens het punt X.
De door Cabri getekende meetkundige plaats is de grafiek van de
functie y = �x2 + 1/x. |
Opdracht 5
| a. |
Teken in dezelfde figuur ook de grafiek van y
= �x2. |
| b. |
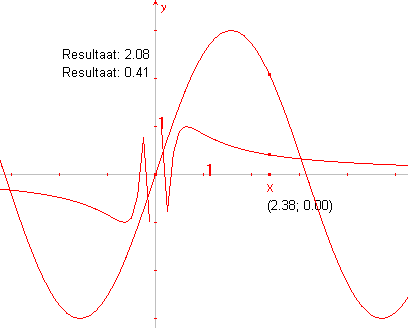
Teken ook de grafieken van de functies y = 3 sin x
en y = sin(1/x) in �en figuur (zie figuur 8a). |
figuur 8a |
|
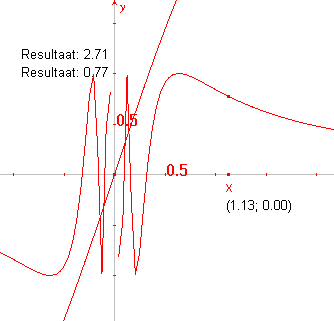
figuur 8b |
 |
|
 |
De grafiek van y = sin(1/x)
heeft in de buurt van x = 0 een wat eigenaardig gedrag.
Je kan daarin wat meer inzicht krijgen, als je de grafiek vergroot.
Dat kan door verplaatsing van de eenheid op de x-as.
| c. |
Selecteer het punt op de x-as dat is
aangegeven met 1 (Deze eenheid).
Sleep dit punt wat meer naar rechts (zie figuur 8b).
Opmerking
Tijdens het verslepen van de eenheid wijzigt de waarde!
[einde Opmerking] |
| d. |
Experimenteer ook eens met enkele andere
functies (naar eigen keuze). |
Download
Dit werkblad is NIET MEER in PDF-formaat beschikbaar.
coords.pdf (ca. 420 Kb)
Een PDF-bestand kan met Acrobat� Reader worden
gelezen: 
[coord.htm] laatste wijziging op:
19-01-18