Constructie ][ Kegelsneden | Macro's voor kegelsneden | Cabri
2. Constructie gebaseerd op lijnvermenigvuldiging van een cirkel
We willen nu op de loodlijn door P op de x-as die de cirkel snijdt in het punt
Q, het punt X construeren waarbij PX = b/a PQ.
Nu is OB = b = b/a OB1.
We kunnen het punt X dus vinden met behulp van de lijn B1Q, die de x-as
snijdt in het punt S, en de lijn SB, die de loodlijn in P snijdt in X.
| figuur 2 | 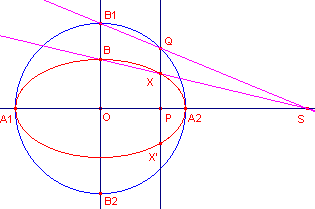 |
Opmerking De cirkel met middellijn A1A2 heet de hoofdcirkel van de ellips. [einde Opmerking] |
In dit geval moeten we wel aantonen, dat de verzameling van de punten X en X' (het
spiegelbeeld van X in de x-as) een ellips is, als P het lijnstuk A1A2
doorloopt.
Op basis van vergelijking van de cirkel met middelpunt O en straal a geldt voor het
punt Q: ![]()
Hierin zijn xQ en yQ de co�rdinaten van het punt Q.
Voor het punt X hebben we nu: 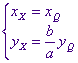 zodat
zodat 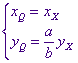 .
.
Substitutie hiervan in bovenstaande betrekking geeft dan:
![]()
Deling van beide leden van de vergelijking door a2 (en
"lopend" maken van de co�rdinaten) geeft dan de vergelijking van de ellips:
![]() .
.
Opmerking
Klik hier ![]() voor een animatie
bij deze constructie.
voor een animatie
bij deze constructie.
[ellips2.htm] laatste wijziging op: 28-12-2000