Hyperbolische meetkunde [6]: Parallelhoek
Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde
1. Formule van Lobatchevski
Vooraf geven we enkele algemeen bekende betrekkingen uit de hyperbolische
goniometrie (zie de pagina "Hyperbolische functies"):
| definitie van de sinus hyperbolicus: | sh x = (ex - e-x) /2 |
| definitie van de cosinus hyperbolicus: | ch x = (ex + e-x)/2 |
| definitie van de tangens hyperbolicus: | th x = sh x / ch x |
ch2 x - sh2 x = 1
sh 2x = 2sh x ch x
ch c = ch a . ch b (stelling van Pythagoras in de hyperbolische meetkunde)
| Stelling 1 In een rechthoekige d-driehoek ABC (C is de rechte hoek) met rechthoekszijden a en b geldt tan A = th(a) / sh(b) (formule van Lobatchevski) |
Bewijs:
We gaan uit van een rechthoekige d-driehoek OAB met A: z = p en B: z =q i.
Eeen dergelijke positionering is voor elke willekeurige d-driehoek via H-afbeeldingen te
bereiken.
Op driehoek OAB passen we een H-afbeelding F toe waardoor A samenvalt met O (zie figuur
1).
| figuur 1 | 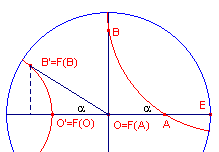 |
Dus: F(z)=(z-p)/(1-pz), zodat F(B) = (qi-p)/(1-pqi) Vermenigvuldiging van teller en noemer met (1+pqi) geeft dan, an enige herleiding: F(B) = -p(1+q2)/(1+p2q2) + i . q(1-p2)/(1+p2q2). Volgende de Euclidische goniometrie is dan tan A = (q(1-p2)) / (p(1+q2) = (1-p2)/p x q/(1+q2) Uit de d-afstandsformule vinden we in driehoek ABC: a = OB = 2arth(q) en b = OA = 2arth(p) zodat q = th(�a) en p = th(�b). |
Nu is (met tanh ipv th):
![]()
en
![]()
(Bij de afleiding van beide uitdrukkingen hebben we van de in het begin van
deze paragraaf genoemde formules gebruik gemaakt).
We vinden dus na vermenigvuldiging:
tan A = th(a) / sh(b) �
Opmerking
Voor kleine waarden van a en b is th(a) = a en sh(b) = b.
Voor kleine driehoeken geldt dus tan A = a/c, hetgeen overeenkomt met de formule in de
Euclidische goniometrie.
[einde Opmerking]
2. Parallelhoek
2.1. P als functie van de lengte van de loodlijn
Uit de formule van Lobatchevski kunnen we een belangrijke vondst van Bolyai en
Lobatchevski afleiden. Deze eigenschap in de hyperbolische meetkunde staat bekend als de parallelhoek.
| figuur 2 | 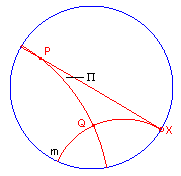 |
|
We kunnen nu stelling 1 gebruiken om de grootte van de parallelhoek uit te drukken in PQ.
| Stelling 2 tan P(PQ) = 1 / sh(PQ) |
Bewijs:
| figuur 3 | 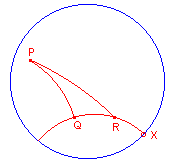 |
In figuur 3 is hoek Q reen rechte hoek van driehoek PQR. In deze driehoek geldt dus tan P = th(QR) / sh (PQ). Indien nu R over de d-lijn nadert naar het punt X, dan nadert th(QR) naar 1, waaruit het gestelde onmiddellijk volgt. � |
Voorbeeld
Zij P : z = � i en zij de lijn m de middellijn door het punt R: z
= 1 (zie figuur 4).
| figuur 4 | 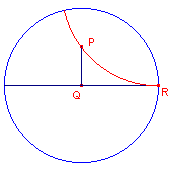 |
Nu is: PQ = 2arth(�) = 1,0986 Voor de parallelhoek bij van P tov. QR vinden we dan, volgens stelling 2: tan P = 1 / sh(PQ) = 1/ sh(1,0986). Zodat hoek P (ongeveer) gelijk is aan 36,9�. [einde Voorbeeld] |
Klik hier ![]() voor een animatie
van Stelling 2.
voor een animatie
van Stelling 2.
2.2. Een constructie van de parallelhoek
We gaan uit van een scherpe d-hoek en construeren de loodlijn op een van de benen van de
hoek die parallel is met het andere been.
| figuur 5 | 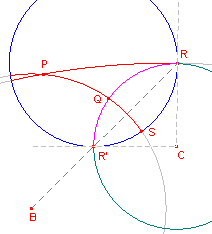 |
We bepalen de loodlijn op het been PS (de drager is cirkel B), terwijl
deze loodlijn parallel is met het been PR. Zij C de gevraagde d-loodlijn. Omdat C loodrecht moet staan op de horizon (en wel in het oneigenlijke punt R), ligt het middelpunt van (de drager van) C dus op de raaklijn in R aan de horizon. Omdat C loodrecht moet staan op PS, en door R gaat, moet het middelpunt van (de drager van) C ook door het inverse punt R' gaan (bij inversie ten opzichte van B). Omdat R op de horizon ligt, ligt R' ook daarop. Het middelpunt van C ligt dus ook op de raaklijn in R' aan de horizon. Het middelpunt van C is dus het snijpunt van beide raaklijnen. Er is dus bij elke scherpe hoek P precies ��n loodlijn die aan de gestelde eisen voldoet. |
Gevolg
Elke scherpe hoek P kan dienen als parallelhoek.
Met andere woorden voor P(PQ) geldt:
0 < P(PQ) <90�
[einde Gevolg]
2.3. De constante van Schweikart
Een bijzondere waarde van de d-afstand PQ krijgen we voor P(PQ) = 45�.
Dan is dus sh(PQ) = 1.
Ferdinand Karl Schweikart (1780-1859) was de eerste die opmerkte dat in een
gelijkbenige rechthoekige d-driehoek de lengte van de d-hoogtelijn op de schuine zijde begrensd
is. Deze grenswaarde wordt de constante van Schweikart genoemd.
We berekenen nu de waarde voor de "grootste" d-driehoek (zie
figuur 6).
| figuur 6 | 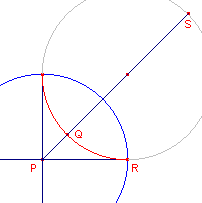 |
We berekenen eerst de Euclidische lengte van PQ: PR2 = PQ . PS of 1 = PQ(PQ + 2), zodat PQ2 + 2PQ - 1 = 0 PQ (eucl) = �(2) -1 d(P,Q) = ln|PQSS')| = ln|(SP/SQ) : (S'P/S'Q)| = ln|(1+�2)/2 : (1/�2)| Waaruit we vinden d(P,Q) = ln(�2+1) |
Overigens geldt een dergelijke begrenzing van de lengte van een d-hoogtelijn in elke
gelijkbenige d-driehoek.
We hebben namelijk:
| Stelling 3 In een d-driehoek ABC met AB (d)= AC heeft de d-lengte van de hoogtelijn uit A een kleinste bovengrens die afhankelijk is van de grootte van hoek A. |
Klik hier ![]() voor een animatie
bij het bewijs van Stellling 3.
voor een animatie
bij het bewijs van Stellling 3.
Bewijs: (zie figuur 7)
| figuur 7 | 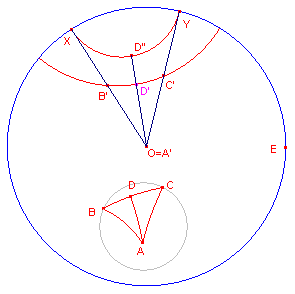 |
We beelden driehoek ABC af met een H-afbeelding, waarbij het beeld van A
samenvalt met het centrum van de disk. Hierbij blijven hoeken en d-lengtes gelijk; dus AD (d)= A'D'. De zijden van ABC worden dan afgebeeld op middellijnen van de disk. Een oneigenlijke punt van A'B' is X en van A'C' is Y. De d-lengte van A'D' is dan kleiner dan de d-lengte van A'D", waarbij D" het snijpunt is van het beeld van de hoogtelijn en de d-lijn die X en Y als oneigenlijke punten heeft. Dus de lengte van AD is kleiner dan de d-lengte van het d-lijnstuk OD", waarbij OD" alleen afhangt van de grootte van hoek XOY, dus van de (daaraan gelijke) hoek A van driehoek ABC.� |
3. Sinus-formule
Het ligt niet in de bedoeling op deze pagina's alle formules voor de hyperbolische goniometrie te behandelen.
We geven hieronder danook nog �en bruikbare formule voor een rechthoekige driehoek.
| Stelling 4 In een rechthoekige d-driehoek ABC (C is recht) met BC = a en AB = c geldt sin A = sinh(a) / sinh(c) |
Bewijs:
In de Euclidische goniometrie hebben we:
als tan A = t, dan is sin2 A = t2 / (1 + t2).
Met gebruikmaking van stelling 1 is dan
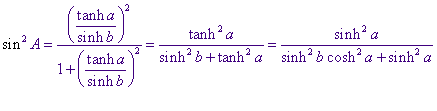
Uitwerking van de noemer N van deze laatste uitdrukking geeft
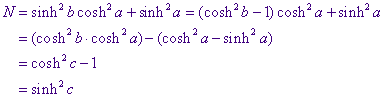
waaruit het gestelde volgt. �
Opmerking
Voor kleine waarden van a en c geldt sh(a) = a en sh(c) = c.
Voor kleine driehoeken geldt du sin a = a/c, hetgeen overeenkomt met de formule in de
Euclidische goniometrie.
[einde Opmerking]
[hypm6.htm] laatste wijziging op: 03-06-2000