Hyperbolische meetkunde [7]: Spiegelingen
Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde
1. Definities
De spiegelingen in de H-meetkunde kunnen min of meer op dezelfde manier worden vastgelegd
als in de E-meetkunde.
We zullen dat hier doen door in eerste instantie alleen de spiegeling van een punt in een
punt en van een punt in een d-lijn te defini�ren.
 |
|
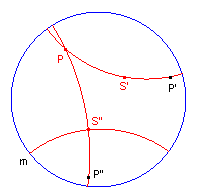
We kunnen eenvoudig bewijzen, dat de spiegeling van een punt in een d-lijn wordt bewerkstelligd door een inversie in de drager van die d-lijn.
| Stelling 1 Is P' het inverse punt van een punt P bij inversie in de d-lijn m, dan is P' het spiegelbeeld van P bij spiegeling in de lijn m. |
Bewijs: zie figuur 1.
| figuur 1 | 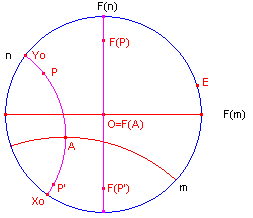 |
[1e bewijs] We hebben d(P,A) = ln|(P,A;Xo,Yo)|. De dubbelverhouding is invariant onder inversie, dus geldt: d(P,A) = ln|(P,A;Xo,Yo)| = ln|(P',A';Yo,Xo)| = d(P',A').� [2e
bewijs] |
Zie ook de animatie bij een lijnspiegeling.
2. Constructies
2.1. Het centrum bij een puntspiegeling
In de E-meetkunde wordt bij gegeven punten P en P' die elkaars beeld zijn bij een
puntspiegeling, het centrum van de puntspiegeling geconstrueerd als midden van het
lijnstuk PP'. Constructie van dat punt gebeurt dan met behulp van de middelloodlijn.
In de P-meetkunde kunnen op dezelfde manier te werk gaan.
| figuur 2 | 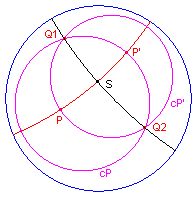 |
We tekenen de d-cirkels (P, PP') en (P', P'P), zie figuur 2. Deze d-cirkels snijden elkaar in de punten Q1 en Q2 die dan ook de middelloodlijn van het d-lijnstuk PP' bepalen. Het snijpunt S van PP' en Q1Q2 is dan het gevraagde centrum. |
Klik hier ![]() voor een animatie
van een hyperbolische puntspiegeling.
voor een animatie
van een hyperbolische puntspiegeling.
2.2. De as bij een lijnspiegeling
Uit paragraaf 2.1 volgt dat spiegelas van een lijnspiegeling waarbij P
op P' wordt afgebeeld, op dezelfde manier kan worden gevonden.
Die as is de d-middelloodlijn van het d-lijnstuk PP' (zie eveneens figuur 2).
In figuur 2 staat dus een eenvoudige constructie van de middelloodlijn
van een d-lijnstuk.
Klik hier ![]() voor een animatie
van een hyperbolische lijnspiegeling.
voor een animatie
van een hyperbolische lijnspiegeling.
3. Overdekkingen
Een overdekking (of vlakvulling; Eng. tessalation) is
een opdeling van het vlak met een aantal congruente meetkundige figuren.
Als eenvoudig voorbeeld kunnen we de overdekking nemen van het Euclidische vlak met
vierkanten (het rooster van een rechthoekig co�rdinatenstelsel; een deel daarvan is te
zien als achtergrond van de pagina's op deze website).
Met behulp van spiegelingen kunnen we op eenvoudige wijze een overdekking maken van het hyperbolische
vlak (de disk).
We geven hier als voorbeeld een overdekking met gelijkzijdige d-driehoeken.
We beginnen met een gelijkzijdige driehoek ABC waarvan de hoekpunten oneigenlijke punten
zijn (zie figuur 3).
Daarna spiegelen we deze driehoek in elk van de d-zijden, enzovoorts (zie
figuur 4).
Het bijzondere van deze laatste figuur is, dat daardoor een vlakvulling ontstaat die met
een "Euclidisch oog" bekeken bestaat uit verschillende vormen en groottes.
| figuur 3 | 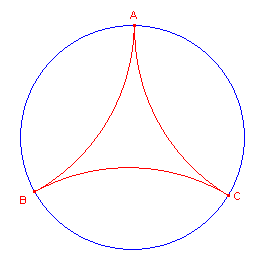 |
figuur 4 | 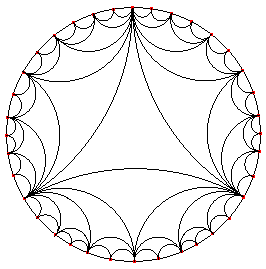 |
Klik hier ![]() voor een animatie
van figuur 4.
voor een animatie
van figuur 4.
4. Referenties
Op het web zijn uiteraard meer pagina's te vinden over hyperbolische meetkunde.
Over vlakverdelingen, zoals vermeld in paragraaf 3:
[1] Vlakverdelingen
in het Poincar�-model (Clark University)
[2] M.C. Escher: Circle
Limit IV - Heaven and Hell (Carol L. Gerten, CGFA / jpeg, ca 190Kb)
[hypm7.htm] laatste wijziging op: 03-06-2000