Hyperbolische meetkunde [8]: Oppervlakte
Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde
1. Asymptotische d-driehoeken
De oppervlakte van een figuur in de E-meetkunde wordt gerelateerd aan de oppervlakte van
een vierkant met zijde 1 (waarvan de oppervlakte per definitie gelijk is aan 1).
Een dergelijke aanpak is in de H-meetkunde niet goed mogelijk.
We bekijken de oppervlakte van d-driehoeken eerst aan de hand van zogenoemde aymptotische
driehoeken.
| enkel(voudig)-asymptotisch | dubbel-asymptotisch | drievoudig-asymptotisch |
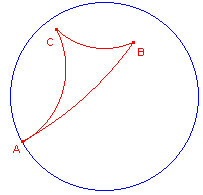 |
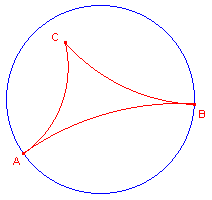 |
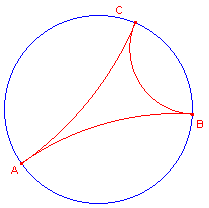 |
We zullen aan de oppervlakte van een d-driehoek de volgende
(gebruikelijke) eisen stellen:
- d-congruente driehoeken moeten gelijke oppervlakte hebben;
- als een d-driehoek gelegen is binnen een andere d-driehoek, dan moet de oppervlakte
ervan kleiner zijn;
- oppervlakte moet additief zijn.
2. Oppervlakte van een asymptotische driehoek
| Stelling 1 Als van twee d-driehoeken ABC en A'B'C' geldt O(ABC) < O(A'B'C'), dan geldt hoekensom(ABC) > hoekensom(A'B'C') |
| figuur1 | 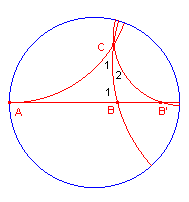 |
Zij B een punt van AB'. Driehoek ABC heeft dus een kleinere oppervlakte dan driehoek AB'C. Nu is in driehoek BB'C: hoek B = 180� - hoek B1 en hoek C2 = hoek C12 - hoek C1. Voor de hoekensom van driehoek BB'C hebben we dus: (180� - B1) + (C12 - C1) + B' < 180� zodat B1 + C1 > B' + C12 waaruit volgt: A + B1 + C1 > A + B' + C12 De hoekensom van de kleinere driehoek is dus het grootst.� |
Gevolg
Erg kleine driehoeken hebben een hoekensom dicht bij 180� (ze zijn bijna Euclidisch).
[einde Gevolg)
| Stelling 2 Een drievoudig-asymptotische driehoek kan worden verdeeld in twee rechthoekige dubbelvoudig-asymptotische driehoeken. |
Bewijs:
| figuur 2 | 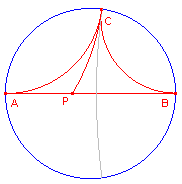 |
We kiezen een punt P op de zijde AB. Valt P samen met A, dan is APC = 180�.. Valt P samen met B, dan is APC = 0�. Er is dus een positie van P op AB waar APC = 90� (het voetpunt van de loodlijn uit C op AB). � |
Bewijs:
| figuur 3 | 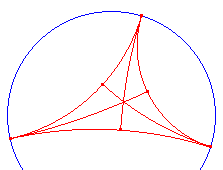 |
Op basis van stelling 2 kunnen we een
drievoudig-asymptotische driehoek verdelen in 6 enkelvoudige-asymptotische driehoeken (met
behulp van de hoogtelijnen; zie figuur 3). Op basis van de optellingseis (zie paragraaf 1) is het dan alleen nodig te bewijzen, dat een enkelvoudig-asymptotische driehoek een eindige oppervlakte heeft. Zij dus ABC een enkelvoudig-asymptotische driehoek, waarbij C een oneigenlijk punt is (A en B zijn dus d-punten).� |
We verlengen AB tot het oneigenlijk punt C' op de horizon.
AD is de d-bissectrice van hoek A, waarbij D op CC' ligt.
We spiegelen (via een H-spiegeling) vervolgens hoek BAC in de lijn AD. Hierbij wordt B
afgebeeld op A1 op AC.
BC wordt dan dus afgebeeld op A1C'.
B1 (op AD) is het snijpunt van BC en A1C' (zie figuur
4).
| figuur 4 | 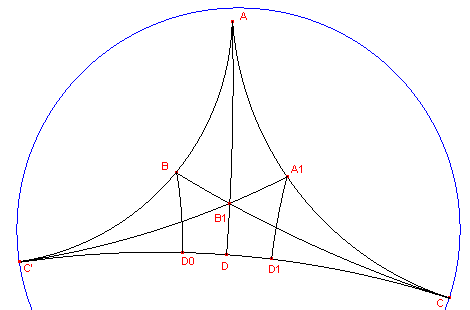 |
De hoeken bij B en A1 voorzien we ook van bisectrices.
We hebben nu een vijfhoek AA1D1D0B; de oppervlakte
daarvan is eindig.
We zullen nu aantonen, dat het mogelijk is driehoek BAC binnen deze vijfhoek af
te beelden.
We doen nu met driehoek B1A1C hetzelfde als we deden met driehoek
BAC: spiegelen in A1D1,
waardoor B1 wordt afgebeeld op A2 (gelegen op CA1) en B1C
wordt afgebeeld op A2C'.
B1C en A1D1 snijden elkaar dan op A1D1
in het punt B2 (zie figuur 5).
| figuur 5 | 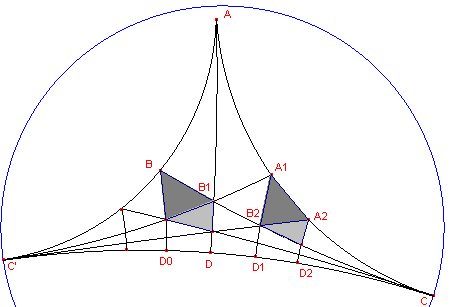 |
In figuur 5 zien we twee paren congruente d-driehoeken, waarvan er
telkens �en gelegen is binnen driehoek BAC en de andere binnen de vijfhoek.
We gaan nu met dit proces door, waardoor we een rij van driehoeken BiAiC
krijgen.
Bij elk tweetal spiegelingen krijgen we dan een paar congruente d-driehoeken waarvan de
ene in driehoek BAC en de ander binnen de vijfhoek ligt.
De enkel-asymptotische driehoek kan dus als serie congruente deeldriehoeken worden
afgebeeld binnen de vijfhoek en heeft dus een eindige oppervlakte.�
| Stelling 4 Twee drievoudig-aysmptotische driehoeken zijn congruent. |
Bewijs:
Een drievoudig-asymptotische driehoek heeft blijkbaar de kleinste hoeksensom (waarde
gelijk aan 0�), en volgens stelling 1 de grootste oppervlakte, die
volgens stelling 3 eindig is.
Hieruit volgt het gestelde.�
3. Oppervlakte van een d-driehoek
We kunnen nu de oppervlaktestelling van de hyperbolische meetkunde bewijzen
Deze stelling is voor het eerst bewezen door Carl
Friedrich Gauss, 1777-1855, Duitsland.
| Stelling 5 - Stelling van Gauss De oppervakte van een d-driehoek ABC met hoeken A,B,C is gelijk aan K(p - A - B - C). Hierbij is K dezelfde constante voor alle d-driehoeken. |
| figuur 6 | 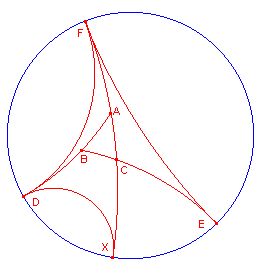 |
figuur 7 | 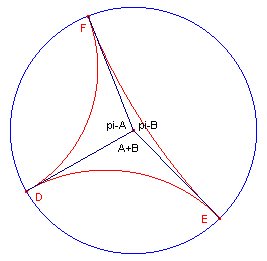 |
We verlengen de zijden AB, BC, CA tot AD, BE, CF waarbij D,E,F op de horizon liggen (zie figuur 6).
Volgens stelling 3 heeft nu driehoek DEF (drievoudig-asymptotisch) een
eindige oppervlakte k.
Elke dubbel-asymptotische driehoek (zoals ADF) heeft een oppervlakte die alleen
afhankelijk is van de "tophoek".
De oppervlakte van driehoek ADF is dus afhankelijk van de hoek p-A.
en dus ook van A.
Stel O(ADF) = f(A)
Verlengen we AC nu tot AX (met X oneigenlijk punt), dan is DFX drievoudig-asymptotisch en
opgebouwd uit twee dubbel-asymptotische driehoeken, zodat
[1]..... k = f(A) + f(p
- A)
We verdelen nu een drievoudig-asymptotische driehoek in drie dubbel-asymptotische
driehoeken met tophoeken p - A, p - B en A + B (zie figuur
7).
Dus
k = f(A) + f(B) + f(p - (A+B))
Nu is f(p - (A+B)) = k - f(A+B),
volgens betrekking [1].
Zodat
k = f(A) + f(B) + k - f(A+B)
Waaruit weer volgt:
f(A) + f(B) = f(A+B)
De functie f is dus lineair, zodat f(A) = pA, waarbij p een constante
is.
De vergelijking [1] gaat hierdoor over in
k = pA + p(p - A)
waarui volgt dat p = k / p.
Dus:
f(A) = kA / p.
In figuur 6 hebben we nu
O(ABC) = O(DEF) - O(AFD) - O(BDE - O(CEF)
zodat we nu vinden
O(ABC) = k - (f(A) + f(B) + f(C) ) =
k - (k/p) (A + B + C) = (k/p) (p - (A + B + C).
Stellen we K = k/p, dan is dus
O(ABC) = K(p - (A+B+C))
Het is gebruikelijk de waarde van K gelijk aan 1 te nemen.
Hierdoor is de oppervlakte van een drievoudig-asymptotische driehoek gelijk aan p.
Zodat
O(ABC) = p
- ( A + B + C)
�
Klik hier ![]() voor een animatie
van de oppervlakte van een d-driehoek.
voor een animatie
van de oppervlakte van een d-driehoek.
[hypm8.htm] laatste wijziging op: 03-06-2000