PseudoCentraal

Cabri werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri

Overzicht - Een punt "tussen" twee cirkels

Formulering van het probleem
Opdracht 1

Intermezzo
Deel 1
Deel 2

(Op weg naar) de oplossing
Opdracht 2
Opdracht 3

Macro:PseudoCentraal
Opdracht 4

Finale
Opdracht 5
Opdracht 6 - Gemeenschappelijke raaklijn aan twee cirkels

Download

Formulering van het probleem
We gaan uit van twee willekeurige cirkels M₁ en M₂ en een willekeurig punt P.
We zoeken een lijnstuk waarvan P het midden is en waarvan de eindpunten op de beide cirkels liggen (zie figuur 1).

figuur 1

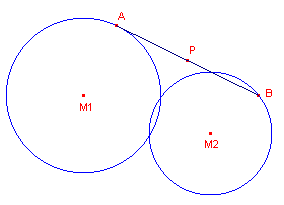Zo’n lijnstuk noemen we in hetgeen volgt de "pseudo-centraal" van de beide cirkels. Het punt P noemen we het "pseudo-midden" van de cirkels.

Opdracht 1

Teken twee cirkels M₁en M₂ en een punt P op een nieuw Cabri-werkblad.
Kies het punt A op cirkel M₁.

Waar ligt het andere eindpunt van de pseudo-centraal nu?
Geef op basis van de formulering van het probleem een tweeledig antwoord op deze vraag.

Op basis van de bestaande constructie op het werkblad is het mogelijk het punt B te construeren dat aan ��n van beide voorwaarden voldoet, namelijk B = Puntspiegeling(A, P).

Construeer het punt B met de functie "Puntspiegeling" in het Afbeeldingen-menu.
Teken ook het lijnstuk AB.
Beweeg nu het punt A over de cirkel M₁.

Wat voor soort kromme lijn beschrijft het punt B in dit geval?

Geef een zo nauwkeurig mogelijke beschrijving van die kromme.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

(*)

(*)

Voor het ophalen van de figuur in Cabri Geometry is het noodzakelijk dat Cabri II is ge�nstalleerd op het gebruikte computersysteem, waarbij de Map-opties voor "Cabri-g�om�tre II Figure" en "Cabri-g�om�tre II Macro" op de juiste wijze zijn ingesteld.
Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren.
Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download).

Intermezzo

Deel 1
Als je het antwoord op de laatste vraag van opdracht 1 niet hebt kunnen vinden, dan kan je een belangrijke functie van Cabri gebruiken, waardoor je wellicht wel tot een antwoord komt.
Heb je wel een antwoord gegeven, ga dan verder met Deel 2 van dit Intermezzo.

Kies in het Constructie-menu de functie "Meetkundige plaats".
Selecteer nu eerst het punt B en daarna het punt A.

Nu wordt de "baan" van het punt B getekend als A over de cirkel beweegt.

Ga dat na door A zelf over de cirkel te "slepen".

Geef nu het antwoord op de laatste vraag van opdracht 1.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Deel 2

Bewaar je huidige werkblad nu voor alle zekerheid op disk met de functie "Bewaar" in het Bestand-menu.
Kies een nieuw Cabri-werkblad (je oude werkblad blijft gewoon bereikbaar).
Gebruik de functie "Nieuw" in het Bestand-menu.

figuur 2

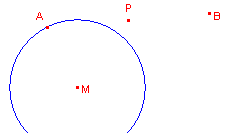Teken een cirkel met middelpunt M en opnieuw een punt P.
Kies het punt A weer op de cirkel en construeer ook B (zie figuur 2).
Bepaal het beeld van cirkel M onder de "Puntspiegeling" met P als centrum.
Kies daartoe de functie "Puntspiegeling" in het Afbeeldingen-menu, selecteer de cirkel (Spiegel deze cirkel) en selecteer dan het punt P (in dit object).
Kies nu weer je eerste werkblad (klik dit bestand aan in het Venster-menu).
Voer nu op dit werkblad dezelfde constructie uit als hierboven.
Wat valt je nu op?
Selecteer de meetkundige plaat en druk op de Del-knop.

Het voordeel van het tot je beschikking hebben van een door Cabri geconstrueerde kromme lijn boven een door Cabri berekende kromme lijn (de meetkundige plaats) is, dat je met de geconstrueerde kromme lijn snijpunten met andere objecten kunt bepalen (dat helaas kan niet met meetkundige plaatsen).

(Op weg naar) de oplossing

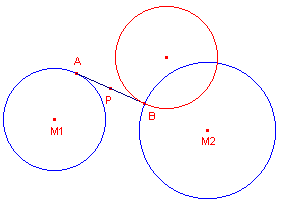
Je kunt nu de oplossing van het probleem gemakkelijk vinden door cirkel M₂te snijden met het gevonden beeld (het beeld van cirkel M₁). Zie daartoe figuur 3.

figuur 3

Opdracht 2

Als er geen oplossing van het probleem is, verplaats dan het punt P of vergroot/verplaats de cirkel M₂.

Formuleer nu wanneer en hoe het probleem van het vinden van de pseudo-centraal van twee cirkels bij een gegeven punt P kan worden opgelost.
Wat is het maximale aantal oplossingen (het maximaal aantal pseudo-centralen) van het probleem? Verklaar je antwoord.
Wanneer is er slechts ��n pseudo-centraal te vinden?

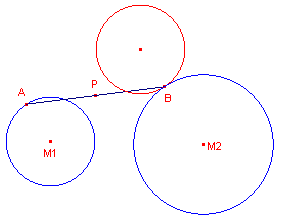
In figuur 4 is een situatie weergegeven waarin er slechts ��n pseudo-centraal van de cirkels (bij het gegeven punt P) te vinden is.

figuur 4

Opdracht 3

Bij vaste ligging en grootte van cirkel M₁ en van het punt P, zijn er meerdere cirkels M₂ (met vaste straal) mogelijk waarbij precies ��n pseudo-centraal bestaat.

Wat is de meetkundige plaats van de middelpunten van die cirkels?
Geef een zo volledig mogelijke beschrijving van die meetkundige plaats (let op: er zijn twee mogelijkheden!).
Aanwijzing
Kies in het Extra-menu (het tweede menu van rechts) de functie "Spoor aan/uit" en selecteer het punt M₂.
Selecteer opnieuw het punt M₂ en sleep het punt M₂ nu zo, dat er steeds maar ��n pseudo-centraal getekend kan worden.
Zet hierna Spoor weer uit.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Macro:PseudoCentraal

Het is handig als je voor verder onderzoek de beschikking hebt over een macro die, uitgaande van de cirkels M₁ en M₂ en het punt P, de pseudo-centralen tekent. We geven deze macro de naam PseudoCentraal.
We moeten dan natuurlijk een figuur gebruiken waarin het maximaal aantal pseudo-centralen is getekend (zie figuur 5).

figuur 5

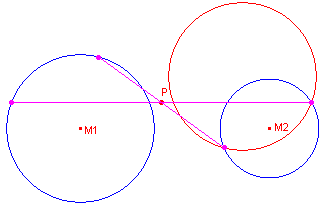Nb.
Bij de constructie van de pseudo-centralen van P ten opzichte van beide cirkels in figuur 5 is het punt A niet gebruikt.

Opdracht 4

Construeer de macro:PseudoCentraal die, uitgaande van twee cirkels M₁ en M₂ en van een punt P, de pseudo-centralen van P ten opzichte van die beide cirkels construeert.

Bewaar deze macro indien gewenst op disk.

Geef een korte beschrijving van de constructie van de macro.
Aanwijzing
Ga uit van de snijpunten van cirkel M₂ met de beeldcirkel van M₁ en construeer op M₁ de andere eindpunten van de pseudo-centralen (gebruik voor dit laatste een afbeelding!).
Beginobjecten: cirkels M₁, M₂, punt P
Eindobjecten: twee lijnstukken (de beide pseudo-centralen).

Finale

We passen in opdracht 5 de macro:PseudoCentraal toe.
Opdracht 5

figuur 6

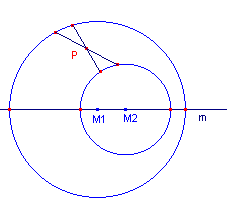Teken een lijn m met daarop de middelpunten M₁ en M₂ van de cirkels. Teken ook het punt P (dichter bij cirkel M2 dan bij cirkel M1). Zie figuur 6 voor de beginpositie van de objecten.
Pas nu de macro:PseudoCentraal toe op P, cirkel M₁ en cirkel M₂.

Als het goed is, zie je twee pseudo-centralen van P ten opzichte van de cirkels.

Geef nu P enkele andere posities en bekijk daarbij het aantal pseudo-centralen.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

figuur 7

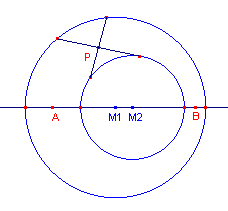In figuur 7 zijn de punten A en B pseudo-middens van de cirkels M₁ en M₂.
Door A en B gaat precies ��n pseudo-centraal.

Waarom zijn A en B pseudo-middens en waarom hebben de cirkels precies ��n pseudo-centraal ten opzichte van A en ten opzichte van B?
Zijn er meer punten "tussen beide cirkels" zoals A en B? Verklaar je antwoord.
Bepaal nu de gebieden waarvoor geldt, dat er, als P in zo’n gebied ligt, twee pseudo-centralen van P zijn ten opzichte van beide cirkels.

Aanwijzing

₁

₂

Geef een zo nauwkeurig mogelijke beschrijving van de gebieden met opvolgend 0, 1 en 2 pseudo-centralen.

Opdracht 6 - Gemeenschappelijke raaklijn aan twee cirkels

Onder een gemeenschappelijk raaklijnstuk van twee cirkels verstaan we het lijnstuk dat de raakpunten op dezelfde gemeenschappelijke raaklijn aan die cirkels verbindt.
In figuur 8 zijn de gemeenschappelijke raaklijnstukken aan de cirkels M₁ en M₂ getekend.

figuur 8

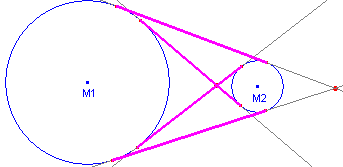Doe een uitspraak over deze gemeenschappelijke raaklijnstukken in verband met pseudo-centralen.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

In figuur 9 zijn cirkels (ze hebben hetzelfde middelpunt!) getekend die in het midden van die raaklijnstukken raken aan de gemeenschappelijke raaklijnen van de cirkels M₁ en M₂.

figuur 9

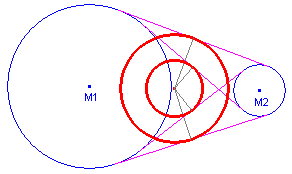Doe een uitspraak over deze cirkels in verband met pseudo-centralen.

Download
De in het werkblad gebruikte Cabri-figuren kunnen via deze website in ��n bestand worden gedownload.
Naast de figuren is ook de gebruikte macro in het bestand opgenomen.
Klik hier om het downloaden van het bestand te starten [12Kb, ZIP-formaat].

Het werkblad zelf is ook in PDF-formaat beschikbaar:
pseudocent.pdf [52Kb]

[pseudocent.htm] laatste wijziging: 17-02-2000