Cabri werkblad - Fagnano

Cabri werkblad

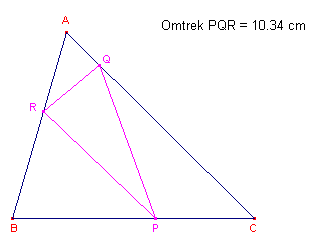Overzicht ][ Alle werkbladen | Meetkunde | Cabri

Overzicht - Fagnano's probleem

Formulering van het probleem
Opdracht 1
Opdracht 2
Download

Formulering van het probleem
In 1775 formuleerde Fagnano (Giovanni F. Fagnano dei Toschi, 1715-1797, Itali�) het volgende probleem:

Construeer in een gegeven scherphoekige driehoek ABC een driehoek PQR (P op BC, Q op CA, R op AB) waarvan de omtrek zo klein mogeljk is.

Fagnano zelf leverde het bewijs met behulp van de differentiaalrekening. Hieronder zullen we het bewijs trachten te leveren met behulp van elementaire meetkunde (en Cabri Geometry).

Opdracht 1

figuur 1

Ga uit van drie punten A, B, C en drie lijnstukken die de zijden vormen.
Kies P, Q, R op de drie zijden (zie figuur 1) met de functie "Punt op object" in het Teken-menu.
Teken daarna driehoek PQR met de functie "Driehoek" in het Teken-menu.

Cabri heeft een functie waarmee de omtrek van een object (in dit geval driehoek PQR) kan worden berekend.

Kies "Afstand en lengte" in het Reken-menu en selecteer daarna driehoek PQR (deze driehoek).
Probeer nu door herhaalde verplaatsing van de punten P,Q en R de minimale omtrek te vinden.
Teken ook de hoogtelijnen van driehoek ABC.

Kan je nu (als je de minimale omtrek denkt gevonden te hebben) iets zeggen over de ligging van de punten P,Q en R met betrekking tot deze hoogtelijnen?

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

(*)

Voor het ophalen van de figuur in Cabri Geometry is het noodzakelijk dat Cabri II is ge�nstalleerd op het gebruikte computersysteem, waarbij de Map-opties voor "Cabri-g�om�tre II Figure" en "Cabri-g�om�tre II Macro" op de juiste wijze zijn ingesteld.
Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren.
Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download).

Opdracht 2

figuur 2

Kies een nieuw werkblad.
Teken opnieuw driehoek ABC en de punten P,Q en R als in figuur 1.
Teken driehoek PQR met behulp van de lijnstukken PQ, QR en RP (met de functie "Lijnstuk" in het Teken-menu).
Spiegel nu het lijnstuk PQ in AC en het lijnstuk PR in AB, beide met de functie "Spiegeling" in het Afbeeldingen-menu (druk eventueel op toets [F1] - Help, waardoor je kan lezen in welke volgorde je de objecten moet selecteren).
Noem de beeldpunten van P opvolgend P₁ en P₂ (zie figuur 2), en teken het lijnstuk P₁P₂.
Bepaal de lengte van P1P2 met de functie "Afstand en lengte" in het Reken-menu.

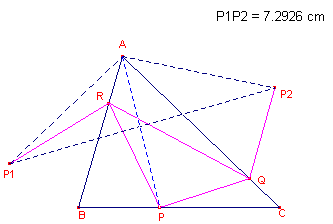Waaraan is het gebroken lijnstuk P₁RQP₂ gelijk? Waarom?
Is het mogelijk Q en R zo te kiezen, dat P₁RQP₂ gelijk wordt aan P₁P₂? Zoja, hoe dan?
Waaraan is P₁P₂ dan eveneens gelijk?

Teken nu ook de lijnstukken AP₁, AP₂ en AP.

Toon aan dat AP₁ = AP en ook dat AP₂ = AP.
Bewijs dat hoek P₁AP₂ = 2 ^. hoek BAC.
Iemand beweert nu:
"De zijde P₁P₂ van de gelijkbenige driehoek P₁AP₂ is zo klein mogelijk, als AP zo klein mogelijk is".
Geef een argumentatie voor de juistheid van deze bewering.
Aanwijzing:
Verandert hoek P₁AP₂ in de gelijkbenige driehoek P₁AP₂, als de positie van P op AB gewijzigd wordt?

Kies P nu op AB zodat AP zo klein mogelijk is. Pas daarbij, indien nodig, de ligging van de punten Q en R aan.

Conclusie:
De driehoek die de kleinste omtrek heeft, is de voetpuntsdriehoek van (het hoogtepunt) van driehoek ABC.

Controleer dit door opnieuw de hoogtelijnen van driehoek ABC te tekenen.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Download
De hierboven behandelde figuren kunnen ook als ��n bestand via deze website worden gedownload.
Dit bestand bevat ook een figuur waarin een tweede bewijs van de "Stelling van Fagnano" wordt gegeven.
Klik hier om het downloaden te starten [6Kb, ZIP-formaat].

[fagnano.htm] laatste wijziging op: 09-11-1999