Cabri werkblad
Overzicht ][ Alle werkbladen | Andere
benaderingen | Meetkunde | Cabri
Zie ook: "Kochansky's
benadering"
Overzicht - Kochansky's benadering van p
- Inleiding
- Vooraf: Cabri's rekenmachine
Opdracht 1
- De constructie van Kochansky
Opdracht 2
- De berekening
Opdracht 3
Opdracht 4
- Download
- Referenties
1. Inleiding
De verhouding tussen de omtrek en de middellijn van
de cirkel wordt gegeven door het getal p .
Dit getal is een zogenoemd trancendent getal (trancendente getallen zijn bijzondere
re�le getallen), hetgeen wil zeggen, dat het geen oplossing is van een
vergelijking met gehele co�ffici�nten).
Daardoor is het niet mogelijk met passer en liniaal een lijnstuk te construeren
waarvan de lengte gelijk is aan p .
Door de eeuwen heen heeft men getracht benaderingsconstructies van p te vinden, en de daarmee
samenhangende vergelijkingen op te stellen.
In 1685 vond de Poolse jezu�tenpater Adam Kochansky (hij leefde van 1635
tot 1700) een dergelijke constructie.
Deze constructie en de daarbij behorende vergelijking zijn onderwerp van dit
Cabri-werkblad.
2. Vooraf: Cabri's rekenmachine
We kijken eerst eens hoe we de waarde van p direct met Cabri kunnen
berekenen (eigenlijk is dat ook benaderen).
Opdracht 1
| figuur 1 |
 |
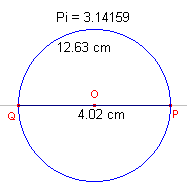Kies een nieuw werkblad.
Teken een lijn met daarop het punt O.
Kies het punt P op die lijn en teken de cirkel met middelpunt O die door P gaat.
Teken het lijnstuk PQ dat de middellijn is waarop P ligt (zie figuur 1).
Kies nu in het Reken-menu de functie "Afstand en lengte".
Wijs PQ aan en bereken de lengte.
Wijs de cirkel aan en bereken de lengte (de omtrek dus).
Merk op, dat de lengtes worden berekend met een bepaalde lengte-eenheid (de cm is de
standaard eenheid van Cabri voor lengte).
Willen we nu de verhouding tussen PQ en de omtrek berekenen, dan zullen we een deling
moeten uitvoeren.
- Dit kan met de functie "Rekenmachine" in het Reken-menu (zie
figuur 2).
| figuur 2 |
 |
Klik in het linker venster van de Rekenmachine, het edit-venster. Hierdoor
kan een variabele in het venster worden geplaatst.
Wijs nu op het werkblad het getal aan (Dit getal) dat de omtrek aangeeft en klik.
Je ziet, dat het getal op het werkblad wordt aangegeven met de letter "a". Deze
"a" wordt ook in het venster van de rekenmachine geplaatst.
Klik nu op de knop [/] van de rekenmachine (dat is de tweede knop van rechts):
"deel door".
Klik nu het getal aan dat de lengte van de middellijn weergeeft. Dit getal is de
variabele "b".
In het edit-venster staat nu "a / b".
- Klik nu op de knop [=]; dat is de knop tussen de beide vensters van de Rekenmachine. In
het rechter venster (het resultaat-venster) komt nu de uitkomst van de berekening.
- Klik nu in dat venster en beweeg de wijzer naar de positie op het Cabri-werkblad waar je
de uitkomst wil plaatsen.
- Klik daar.
Als het goed is staat er nu een tekst als "Resultaat: 3,14" op het werkblad
(zie nogmaals figuur 1, waarin "Resultaat:" is vervangen door
"Pi =").
Opmerking
Het aantal decimalen van een getal kan worden vergroot of verkleind door het getal te
selecteren (je ziet "Dit getal"), dan 1 keer klikken en daarna op de
grijze [+] knop of op de grijze [-] knop te drukken (rechts op het toetsenbord).
[einde Opmerking]
3. De constructie van Kochansky
Opdracht 2
Kies een nieuw werkblad met daarop een punt O.
Teken een horizontale lijn door O. Kies op deze lijn een punt P.
Teken het lijnstuk OP. (De lengte van) dit lijnstuk wordt later gebruikt.
Teken ook de lijn door O loodrecht op de horizontale lijn (zie figuur 3).
Construeer nu achtereenvolgens de punten A (met de cirkel door O en P), B, E, C en D.
| figuur 3 |
 |
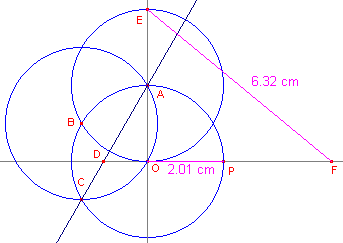Construeer nu het punt F op de horizontale lijn zodat DF = 3OP.
Aanwijzing
Je kan hierbij wellicht gebruik maken van het lijnstuk OP en mogelijk ook van twee
puntspiegelingen.
[einde Aanwijzing]
- Teken het lijnstuk EF en laat Cabri daarvan de lengte bepalen.
- Bereken nu de verhouding tussen de lengtes van EF en OP.
- Welk getal heb je gevonden? Is het iets als 3,14?
- Ga na, dat door verplaatsing van P over de horizontale lijn het gevonden getal niet
verandert.
Je hebt nu Kochansky's benadering van
p geconstrueerd.
Klik
hier voor de pagina "Kochansky's benadering", waarop een animatie
van de constructie staat met CabriJava.
4. De berekening
In figuur 4 zien we een (vergroot) stukje
van figuur 3.
| figuur 4 |
 |
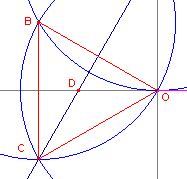Opdracht 3
Wat voor soort driehoek is OBC (zie figuur 3 of figuur 4)?
Waarom?
Waarom staat OB loodrecht op de lijn door C en D?
Het punt D is een bijzonder punt van driehoek OBC. Welk bijzonder punt?
Stel nu de lengte van OP gelijk aan
x.
x?
Druk nu OD in x uit.
Druk ook OF en daarna EF in x uit.
Toon nu aan, dat de verhouding tussen EF en OP gelijk is aan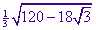 
Bereken, bijvoorbeeld met de grafische rekenmachine, de waarde van
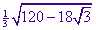in 6 decimalen.
Hoeveel verschilt deze waarde van de werkelijke waarde van p ?
Opdracht 4
Stellen we nu
x =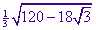
x voldoet
aan de vergelijking:
9x4 - 240x2 + 1492 =0
Dit is de vergelijking die bij de
p -benadering van Kochansky hoort.
- Bereken ook de andere oplossingen (wortels) van de "vergelijking van
Kochansky".
5. Download
Van dit werkblad is ook een versie in PDF-formaat beschikbaar:
benpi3work.pdf
[38Kb]
6. Referenties
[1] Klik hier voor de pagina "Kochansky's
benadering" (met onder meer een benadering mbv. Maple4).
[2] Op de pagina "De oppervlakte van een cirkel"
op deze website staan enkele links naar
andere informatie over p op het Internet.
[3] Zie verder ook de pagina "Benaderingen van p" op deze
website.
[benpi3work.htm] laatste wijziging op: 17-02-2002