Benadering van p volgens Kochansky
Inleiding | Met Maple | Meetkundig | Download ][ Overzichtspagina | Meetkunde
Zie ook: Cabri-werkblad over Kochansky's benadering van p
0. Inleiding
De Poolse jezu�zietenpater Adam Kochansky (1631-1700) heeft in 1685 een
benadering van p gevonden.
Merkwaardig is, dat deze benadering niet vaak wordt genoemd in overzichten van de
verschillende in de tijd gevonden benaderingen.
We geven onderstaand twee methodes voor Kochansky's benadering:
1. Methode met Maple
We gaan allereerst uit van de vergelijking 9x4 - 240x2 +
1492 = 0.
Het blijk dat ��n van de wortels van deze vergelijking een aardig nauwkeurige benadering
van de waarde van p geeft.
> restart: > verg := 9*x^4-240*x^2+1492=0;
verg := 9x4-240x2+1492 = 0
> oplossing := { solve(verg, x) };
oplossing := { 1/3�(120 + 18�3), -1/3�(120 + 18�3), 1/3�(120 - 18�3), -1/3�(120 - 18�3) }
> pi_kochansky := oplossing[3];
pi_kochansky := 1/3�(120 - 18�3)
> evalf(",15);
3.14153333870509
> evalf(Pi-pi_kochansky);
.000059316
We vinden dus een benadering van p waarvan de fout kleiner is dan 10-4.
2. Meetkundige
constructie
Met behulp van passer en liniaal is dezelfde benadering als in paragraaf 1
ook te construeren.
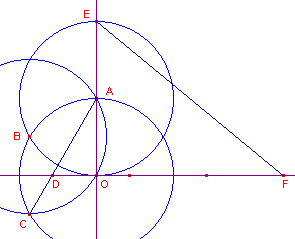 |
In de hiernaast staande figuur is een orthogonaal assenstel Oxy
gedefinieerd. Daarin is OA = AE = 1. De cirkels met middelpunten O en A, beide met straal 1, snijden elkaar in het punt B. De cirkel met middelpunt B en eveneens met straal 1 snijdt de cirkel met middelpunt O ook in het punt C. De lijn AC snijdt de x-as in het punt D. Het punt F ligt zo op de x-as, dat DF = 3. Nu is EF = 1/3�(120 - 18�3) We vinden op deze manier dezelfde benadering voor p als in paragraaf 1. |
Klik hier ![]() voor een animatie van de constructie met behulp van
CabriJava.
voor een animatie van de constructie met behulp van
CabriJava.
Zie ook het Cabri-werkblad
waarop deze benadering wordt behandeld.
Op dit werkblad wordt ook de equivalentie van de methoden in paragraaf 1
en paragraaf 2 behandeld.
3. Download
Het in paragraaf 1 gebruikte Maple werkblad (Maple R4) kan via deze
website worden gedownload.
Klik hier om het downloaden te starten
[ZIP-formaat, ca. 1Kb].
[benpi3.htm] laatste wijzing op: 06-06-2000