Cabri-FAQ (27)

[ Alle Vragen | Meetkunde | Cabri ]

Vorige

Begin

Volgende

Vraag 27
Hoe kun je het "kleven" van cirkelsnijpunten voorkomen?

Antwoord
Allereerst maar een toelichting op het probleem.

figuur 1

figuur 2

In figuur 1 zijn getekend: - de cirkel (A, AB); - de middelloodlijn m van het lijnstuk AB; - een variabel punt X op m; - de omcirkel van driehoek XAB; - het tweede snijpunt Y van de beide cirkels. Dit snijpunt is aangewezen met de Cabri-functie "Punt" (of met "Snijpunt(en)"; tekst op het tekenscherm: Dit snijpunt). Na verplaatsing van het punt X op de lijn m kan nu de situatie ontstaan als in figuur 2: Het punt Y blijft dan samenvallen met ("kleven" aan) het punt B (de positie van het oorspronkelijk tweede snijpunt van de cirkels). Het tweede snijpunt wordt in dit geval niet (meer) weergegeven.

Opmerking
Dat X op de middelloodlijn van AB ligt is niet van wezenlijk belang.
[einde Opmerking]

Klik hier voor een CabriJavapplet ter illustratie van het bovenstaande.

Oorzaak
De oorzaak van het verschijnsel is, dat Cabri onderscheid maakt tussen het eerste en tweede snijpunt van twee objecten. Het punt Y wordt in dit geval als eerste snijpunt aangemerkt. Het tweede snijpunt bestaat nog niet, maar valt samen met B. Bij verplaatsing van het punt X komt Y in de buurt van het tweede snijpunt en uiteindelijk passeren de snijpunten elkaar.

Klik hier voor een CabriJavapplet waarmee dit passeren nog eens wordt ge�llustreerd.

Oplossing
Het probleem kan worden opgelost door gebruikt te maken van een macro waarmee het tweede snijpunt wordt geconstrueerd.
Klik hier voor een CabriJavapplet waarmee dit wordt ge�llusteerd.
In de applet is gebruik gemaakt van de macro:TweedeCirkelsnijpunt.
De constructiestappen van de macro zijn:

figuur 3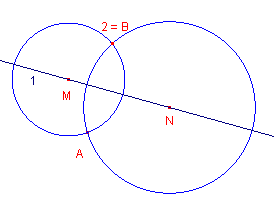

Uitgaande van de cirkels met middelpunten M en N, en een gemeenschappelijk punt A van die cirkels. 1 - Lijn(M, N) 2 - Spiegeling(A, 1) = B Beginobjecten: cirkel M, cirkel N, punt A Eindobject: punt B   Met dank aan Aad Goddijn, Freudenthal Instituut, Utrecht.

Zie Download.

Vorige

Begin

Volgende

[faq27.htm] laatste wijziging op: 02-10-01