1. Inleiding
![]()
Bij de constructie van de gemeenschappelijke raaklijnen aan twee
(niet concentrische) cirkels wordt meestal gebruik gemaakt van de (inwendige en
uitwendige) gelijkvormigheidspunten van die cirkels.
| figuur 1 | 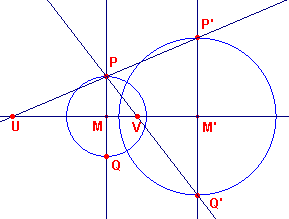 |
 |
De gelijkvormigheidspunten kunnen worden gevonden (zie figuur 1) met
behulp van twee evenwijdige middellijnen PQ en P'Q', beide loodrecht op de centraal MM'
van de cirkels. PP' geeft dan het uitwendig gelijkvormigheidspunt U; PQ' geeft het inwendig gelijkvormigheidspunt V. |
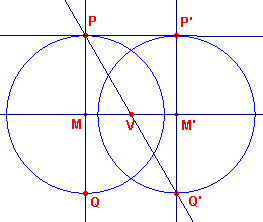
Indien de cirkels gelijke straal hebben, ligt het punt U "op oneindig", terwijl het punt V dan het midden is van het lijnstuk MM'.
Opmerking
De puntenparen (U, V) en (M, M') hebben een harmonische ligging op de centraal.
Ook als U op oneindig ligt, is dit het geval:
het harmonisch vierde punt bij de eindpunten van een lijnstuk en het midden van dat
lijnstuk is het punt op oneiding van de drager van het lijnstuk.
[einde Opmerking]
| Bij de daadwerkelijke constructie van de gemeenschappelijke raaklijnen
maakt men gebruik van een derde (en vierde) cirkel (zie figuur 2). De raaklijnen door het punt U (uitwendige raaklijnen) aan de cirkel M zijn in de figuur geconstrueerd met behulp van de cirkel waarvan het middelpunt het midden van UM is. De raaklijnen door het punt V (inwendige raaklijnen) zijn geconstrueerd met behulp van de cirkel waarvan het middelpunt het midden van VM' is. Deze constructie mislukt echter, als de beide cirkels een gelijke straal hebben. Immers, het punt U ligt dan op oneidig. |
figuur 2 | 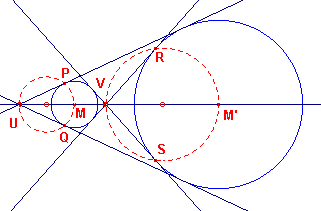 |
In de volgende paragraaf zullen we deze onvolkomenheid trachten te omzeilen.
2. Gebruik
van de machtlijn ![]()
We bewijzen allereerst een eigenschap van de machtlijn van twee
cirkels in samenhang met de gemeenschappelijke raaklijnen aan die cirkels.
Hiertoe bekijken we allereerst figuur 3.
| figuur 3 | 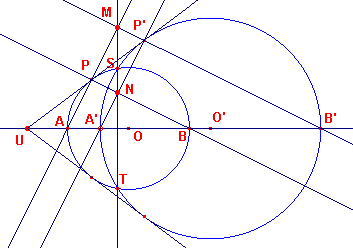 |
In deze figuur is ST de machtlijn van de cirkels O en O'. P en P' zijn
de raakpunten van een uitwendige (gemeenschappelijke) raaklijn aan de cirkels. De bedoelde eigenschap is nu:
Opmerking |
We zullen de genoemde eigenschap bewijzen voor iedere configuratie van de cirkels.
Voorts zullen we laten zien, dat deze eigenschap gebruikt kan worden bij de constructie
van de gemeenschappleijke raaklijnen, ook in het geval, dat de cirkels een gelijke straal
hebben.
Bewijs van de eigenschap genoemd
bij in figuur 3.
We gaan uit van de cirkels op AB (middelpunt O) en A'B' (middelpunt O') , en van de cirkel
met middellijn AB (middelpunt W).
m is de machtlijn van cirkel O en cirkel O'. m snijdt cirkel W in het
punt M (zie figuur 4).
| figuur 4 | 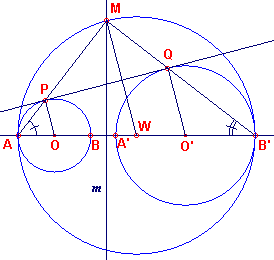 |
figuur 5 | 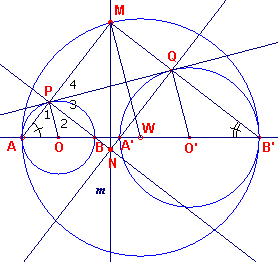 |
Trekken we een lijn door O evenwijdig met MW. Laat P het snijpunt zijn van deze lijn Nu is driehoek AOP' gelijkvormig met driehoek AWM die gelijkbenig is in W. Dus is AOP gelijkbenig in O. Met andere woorden P ligt op cirkel O. Evenzo ligt Q op cirkel O'.
We tonen nu aan dat de lijn door P en Q een gemeenschappelijke raaklijn is van beide
cirkels.
Zie nu figuur 5.
Hierin zijn de lijnen BP en A'Q getrokken, die elkaar snijden in N. Onmiddellijk is nu
duidelijk, dat PNQM een rechthoek is Immers APB en A'QB' zijn rechthoekig in opvolgend P
en Q).
We tonen nu aan, dat ook N op de machtlijn m ligt. We bekijken daartoe de
driehoeken BNA' en B'MA. Deze liggen homothetisch ten opzichte van elkaar (immers de
overeenkomstige zijden zijn evenwijdig). Uit deze gelijkvormigheid volgt nu:
MA / MB' = NA' / BN.
Uit M op de machtlijn van de cirkels volgt: MP . MA
= MQ . MB', zodat (wegens die rechthoek) NQ . MA
= NP . MB'. Uit dit laatste volgt dan
MA / MB' = NP / NQ
Dus NA' / BN = NP / NQ, waaruit we vinden NA' . NQ =
NB . NP. N heeft dus gelijke machten ten opzichte
van beide cirkels.
Dus N ligt op de machtlijn m.
Uit het feit, dat ?A (= ?P3)
het complement is van ?P4 en ?A
ook het complement is van ?P2, volgt dat ?P2 = ?P4.
Dus ?P23 = 90?, waaruit volgt dat PQ raakt aan
cirkel O.
Op dezelfde manier bewijzen we dat PQ ook raakt aan cirkel O'.
PQ is dus gemeenschappelijke raaklijn van de beide cirkels. ?
Opmerking
Het snijpunt van PQ en de machtlijn m (niet met een letter aangegeven in figuur 5) is het midden van het lijnstuk PQ.
[einde Opmerking]
3.1. Uitwendige raaklijnen
![]()
De constructie voor de uitwendige raaklijnen verloopt dus als volgt
Deze constructie voldoet ook voor cirkels die gelijke straal hebben, immers bij het bewijs van de eigenschap in paragraaf 2 is nergens gebruik gemaakt van de lengte van de stralen (in stricte zin). Zie daarvoor figuur 6.
| figuur 6 | 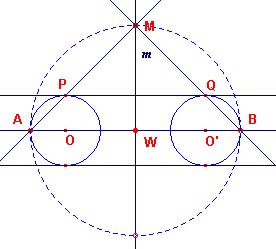 |
figuur 7 | 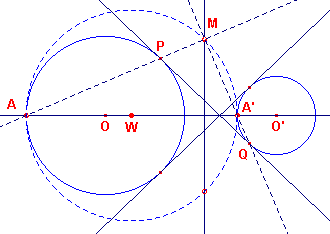 |
3.2. Inwendige raaklijnen ![]()
De constructie voor de inwendige raaklijnen geschiedt op ongeveer dezelfde manier.
Alleen wordt nu gebruik gemaakt van de "grote" cirkel met middellijn AA' (zie figuur 7).
4. Animatie
![]()
Via een animatie kunnen de verschillende configuraties van de beide cirkels worden
bestudeerd.
Klik hier ![]() om de pagina met deze animatie te laden.
om de pagina met deze animatie te laden.
5. Werkblad
![]()
Op deze website staat ook een Cabri-werkblad over raaklijnen:
Raaklijnen : raaklijn aan een
cirkel, raaklijnen aan twee cirkels.
In dat werkblad wordt de gebruikelijke constructie van raaklijnen aan een cirkel
behandeld.