Indien een rechte, op een rechte opgericht, hoeken maakt, zal ze of twee rechte zijn of [hoeken] gelijk aan twee rechte maken.
(vertaling uit: Dr. E.J. DIJKSTERHUIS, De Elementen van Euclides)
Enkele proposities tbv. constructies
Prop I-13 | Prop I-38 | Prop I-42 ][ Elementen | Meetkunde
Deze pagina is opgenomen ten dienste van de pagina "Meetkundige constructies" (B�tasteunpunt voor Scholieren, Rijksuniversiteit Groningen).
| . |
 |
Opmerking Op de moderne lezer maakt deze vertaling mogelijk een wat vreemde indruk. Mogelijk komt zelfs de vraag "Wat wordt hier nu bedoeld?" op. PROKLOS verklaart de zinsnede "Indien ... maakt," met het feit, dat hierdoor uitgesloten wordt dat de opgerichte lijn door het eindpunt van het lijnstuk (voor de Grieken is een rechte lijn een lijnstuk) gaat. De noodzaak om deze stelling te bewijzen is een gevolg van het ontbreken van het begrip "gestrekte hoek". [einde Opmerking] |
Bewijs (vertaling uit het Duits naar CLEMENS
TH�R, Die Elemente, Darmstad, 1975):
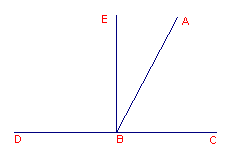
Een rechte lijn AB, opgericht op de lijn CD, vormt de hoeken CBA en ABD.
Ik beweer dat de hoeken CBA, ABD of twee rechte hoeken zijn, of [samen] gelijk zijn aan
twee rechte hoeken.
Is CBA = ABD, dan zijn ze gelijk aan twee rechte hoeken (dit is Definitie 10; dk)
Als dit niet zo is, trek dan BE door B loodrecht op CD; CBE, EBD zijn du twee rechte
hoeken. Hier is CBE = CBA + ABE; daarom voegt men aan beide kanten EBD toe; dan is:
CBE + EBD = CBA + ABE + EBD.
Ook is:
DBA = DBE + EBA; daarom voegt men aan beide kanten ABC toe; dan is:
DBA + ABC = DBE + EBA + ABC
Zoals hierboven bewezen is, is CBE + EBD gelijk aan die drie hoeken.
Wat aan hetzelfde gelijk is, is ook aan elkaar gelijk (Axioma 1). Dus is ook
CBE + EBD = DBA + ABC. Maar CBE, EBD zijn twee rechte [hoeken].
Dus is ook DBA + ABC gelijk aan twee rechte hoeken.
Hetgeen bewezen moest worden. �
| Propositie I-38
Driehoeken op gelijke basis en tussen dezelfde parallelen zijn gelijk aan elkaar. |
| . |
 |
Bewijs (vertaling uit het Duits naar CLEMENS
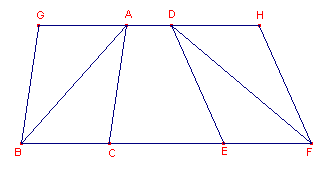
TH�R, Die Elemente, Darmstad, 1975): De driehoeken ABC, DEF liggen op gelijke bases BC, EF tussen dezelfde parallellen BF en AD. Ik beweer dat oppervlakte ABC = oppervlakte DEF. Men verlengt AD naar beide kanten naar G, H, trekt door BG door B // CA en FH door F // DE. |
Dan zijn GBCA en DEFH beide parallelogrammen; en GBCA = DEFH; want ze liggen gelijke
basis BC, EF en tussen dezelfde parallelen (Propositie I-36).
Verder is ABC van GBCA de helft; want deze wordt door de diagonaal AB gehalveerd (Propositie I-34). En FED is de helft van DEFH; want deze wordt
door de diagonaal DF gehalveerd.
De helften van gelijk gehelen zijn aan elkaar gelijk. Dus ABC = DEF.
Hetgeen bewezen moest worden. �
Klik hier ![]() voor een CabriJavapplet
ter illustratie.
voor een CabriJavapplet
ter illustratie.
| Propositie I-42
In een gegeven rechtlijnige hoek een parallelogram te construeren, gelijk aan een gegeven driehoek. |
| . |
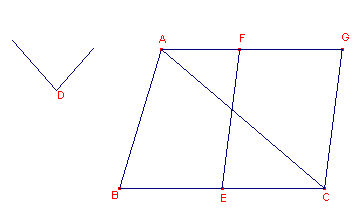 |
Constructie: Zijn gegeven driehoek ABC en hoek D. Dan bepaalt men het midden E van BC, maakt hoek CEF gelijk aan hoek D en trekt AG evenwijdig met BC en CG evenwijdig met EF. Nu is de oppervlakte van driehoek ABC gelijk aan de oppervlakte van CEFH. � |
[propI13.htm] laatste wijziging op: 22-08-03