Generalisatie van de spiegeling: de centrale collineatie
Overzicht ][ Proj.Meetkunde | Meetkunde0. Overzicht ![]()
Puntspiegeling
| figuur 1
|
Zij O een vast punt in het vlak. De puntspiegeling Po van een punt X met Po(X) = X’ wordt vastgelegd door
|
Eigenschappen
De eigenschappen van deze afbeelding zijn genoegzaam bekend. We noemen er enkele.
| figuur 2
|
Zij m een willekeurige rechte lijn in het vlak. De loodrechte lijnspiegeling Lm van een punt X met Lm(X) = X’ in een lijn m wordt vastgelegd door
Opmerking |
Eigenschappen
Ook hier alleen een enkele:
| figuur 3
|
Zijn m en r twee willekeurige lijnen in het vlak
waarbij r niet loodrecht staat op m. We noemen in dit verband de scherpe hoek j tussen de lijnen m en r de richting van de spiegeling. De scheve lijnspiegeling Sm[r] van een punt X met Sm[r](X) = X’ in de lijn m in de richting van een lijn r wordt vastgelegd door
|
Eigenschappen
| figuur 4
|
Zie hiervoor ook het Cabri-werkblad "Scheve lijnspiegeling". De afstand van de punten X en X’ tot de lijn m zijn gelijk, waardoor driehoeken die twee hoekpunten op de lijn m hebben gelijke oppervlakte hebben (zie figuur hiernaast). Daaruit volgt dan gemakkelijk het algemene geval. ? |
Tweede bewijs (analytisch):
| figuur 5
|
We gaan uit van een orthonormaal assenstelsel. De lijn m laten
we samenvallen met de x-as. De basisvectoren zijn dan e1 = (1,0) en e2 = (0,1). Het beeld van e1 is (1,0). Zij Y’ het beeld van het eindpunt Y van e2. We hebben dan Y’ = (x, -1). Voor P, het midden van OQ geldt dan OY/OP = tan j . Zodat uit OP = 1/tan j volgt: x = 2/tan j . |
Voor de determinant van de afbeelding Sm[r] geldt dan:
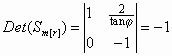
?
| figuur 6
|
|
Klik hier ![]() voor een CabriJavapplet
ter illustratie.
voor een CabriJavapplet
ter illustratie.
Opmerking
Indien de lijn r loodrecht staat op m, dan gaat de scheve lijnspiegeling
over in de loodrechte lijnspiegeling.
Zie verder eventueel ook de pagina "Affiene afbeeldingen"
[einde Opmerking]
| figuur 7
|
O is een vast punt en m is een vaste lijn in het vlak. Het beeld X’ van een punt X bij een centrale collineatie CO,m wordt vastgelegd door (OHXX’) = -1 waarbij H het snijpunt is van de lijn OX en de lijn m. (OHXX’) is de dubbelverhouding Nb. Dat
(OHXX') = -1 is n i e t noodzakelijk voor een centrale
collineatie. Ook als (OHXX') = k (met k constant), spreekt men van een
centrale collineatie. |
Opmerking
Een centrale collineatie wordt ook wel perspectiviteit (of perspectieve
afbeelding) genoemd.
[einde Opmerking]
Eigenschappen
Klik hier ![]() voor een CabriJavapplet
ter illustratie.
voor een CabriJavapplet
ter illustratie.
| Stelling Zij P en p pool en poolijn van een kegelsnede K. Bij de centrale collineatie met centrum P en as p is K (niet-puntsgewijs) invariant |
Bewijs:
| figuur 9a
|
In figuur 9a wordt een punt R?
bepaald door de evenwijdige lijnen r. Door identificatie van O met R? krijgen we dan figuur 9b. Door identificatie van twee punten op m met twee punten op l? krijgen we figuur 9c. |
| figuur 9b
|
figuur 9c
|
[2]
Als m ? l?
, dan gaat de centrale collineatie over in de puntspiegeling met centrum O. Immers uit
(OHXX’) = -1 volgt dan dat O het midden is van het lijnstuk XX’ (voor ieder punt
X).
6. Andere eigenschappen van de centrale collineatie
![]()
| Stelling Een centrale collineatie beeldt een kegelsnede af op een kegelsnede. |
Bewijs:
| figuur 10
|
Een en ander volgt uit de projectieve eigenschappen van een kegelsnede, waardoor projectieve lijnenwaaiers door de centrale collineatie weer worden afgebeeld op waaiers met dezelfde eigenschappen. ? |
Gevolg
Bekijken we nu de vermenigvuldiging V met centrum O en factor ?.
De collineatie-as van de centrale collineatie wordt door V afgebeeld op een rechte lijn m’.
Deze lijn m’ speelt nu een rol om de beelden van de kegelsneden te
onderscheiden in hun verschillende typen: ellips, parabool
en hyperbool.
Immers de punten van de lijn m’ worden door de centrale collineatie
afgebeeld op punten van l? (het beeld van m’
bij de centrale collineatie is l? ).
| figuur 11a
|
figuur 11b
|
figuur 11c
|
In figuur 11a snijdt de lijn m’ de kegelsnede (in dit
geval een cirkel) in twee verschillende punten. Het beeld van de cirkel is dus een
hyperbool.
In figuur 11b raakt de lijn m’ aan de cirkel. Het beeld van de
cirkel is een parabool.
In figuur 11c heeft de lijn m’ geen punten gemeen met de cirkel.
Het beeld is een ellips.
Klik hier ![]() voor een CabriJavapplet
ter illustratie.
voor een CabriJavapplet
ter illustratie.
Asymptoten van een hyperbool
| figuur 12
|
In figuur 12 snijdt de kegelsnede (in dit geval weer een
cirkel) de lijn m in twee punten A en B. Het beeld is dus een hyperbool. De beelden van de punten A en B liggen dus op l? . De raaklijn in A (en B) wordt afgebeeld op de raaklijn in A? (en B? ). De beelden daarvan zijn dus de asymptoten van de hyperbool. Echter, lijn (ic. de raaklijn in A) en beeldlijn (een asymptoot) snijden elkaar op m: het punt A". De lijn door A" evenwijdig aan de lijn OA is dus een asymptoot. De lijn door B" evenwijdig aan de lijn OB is eveneens een asymptoot van de hyperbool. |
Een bijzonder geval
We laten het centrum O van de centrale collineatie samenvallen met het middelpunt van de
cirkel.
| figuur 13a
|
In figuur 13a is de lijn TTm de raaklijn in T aan de cirkel. De lijn T’Tm is dan raaklijn aan (in dit geval) de ellips (het beeld van de cirkel bij de centrale collineatie met centrum O). Deze lijn snijdt de lijn m’ in het punt R. Nu is dus hoek T’OR = 90? . Het punt O is nu een brandpunt van de ellips; de lijn m’ is de daarbij behorende richtlijn. |
| figuur 13b
|
In figuur 13b is de situatie weergegeven voor een parabool (de lijn m’
raakt aan de cirkel). Het punt Q (samen met het punt P snijpunten van de lijn OTm en de cirkel) heeft als beeld het punt Q’ (de top van de parabool). |
| figuur 13c
|
In figuur 13c zien we de situatie voor een hyperbool. |
7. Constructies met Cabri (macro's) ![]()
macro:VierdeHarmonische
| figuur 14a
|
We gaan uit van de (collineaire) punten A, B, C. Construeer nu het punt D zo, dat (ABCD) = -1. 1. Lijn(B, C) 2. Cirkel(C, B) 3. Loodlijn(C, 1) 4. Snijpunt(3, 2) = P 5. Lijn(P, A) 6. EvenwijdigeLijn(B, 5) 7. Snijpunt(6, 3) = Q 8. Puntspiegeling(Q, B) = R |
9. Lijn(P, R)
10. Snijpunt(1, 9) = D
Beginobjecten: A, B, C (in deze volgorde); eindobject: D.
Bewijs:
ACP ~ BCQ (hh), waaruit volgt: AP : BQ = AC : BC
en ook DPA ~ DRB (hh) waaruit volgt: PA : RB = DA : DB.
Dan is
(ABCD) = (CA/CB) : (DA/DB) = (AP/BQ) x
(RB/PA) = -BQ / RB = -1. ?
Gevolg
| figuur 14b
|
Als het punt A samenvalt met het oneigenlijke punt van de
lijn BC, dan is B het midden van CD. In figuur 14b is m een lijn evenwijdig met BC. A is het "snijpunt" van deze lijnen; zie de notatie A= (INF; 0.00). Opmerking |
[einde Gevolg]
macro:CentrCollPunt
Deze macro gebruiken we om snel het beeld van een punt bij een centrale collineatie te
construeren (hier is ook k = -1).
| figuur 15a
|
Constructiestappen uitgaande van de gegeven objecten O, X en m (de collineatie-as): 1. Lijn(O, X) 2. Snijpunt(1, m) = Xm 3. macro:VierdeHarmonische(O, Xm, X) = Y Beginobjecten: X, O (in deze volgorde), m; eindobject: Y. |
| . |
figuur 15b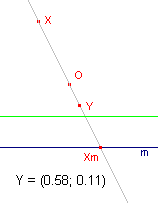 |
figuur 15c
|
Gevolg Als X gelegen is op het beeld van de lijn m bij vermenigvuldiging met ? tov. O, dan is Y het oneigenlijk punt van de lijn OX (zie figuur 15b en figuur 15c). Dan is X het midden van het lijnstuk OXm. [einde Gevolg] |
Op basis van de macro:CentrCollPunt kunnen we nu de macro:CentrCollineatie defini?ren waarmee van andere objecten (zoals lijnstuk, lijn, cirkel, kegelsnede) het beeld bij een centrale collineatie kan worden geconstrueerd.
macro:CentrCollineatie (alleen het beeld van een cirkel; hier is ook k = -1)
figuur 16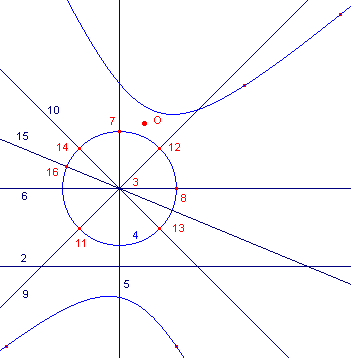 |
Constructiestappen uitgaande van het punt O (1), de lijn m (2)
en een cirkel (middelpunt 3 en lijn 4): 5. Loodlijn(3, 2) 6. Loodlijn(3, 5) 7, 8. Snijpunt(5, 4), Snijpunt(6, 4) 9. Middelloodlijn(1, 8) 10. Loodlijn(3, 9) 11, 12. Snijpunten(9, 4) 13, 14. Snijpunten(10,14) 15. Middelloodlijn(7, 11) 16. Snijpunt(15, 4) 17. (geen nummer) macro:CentrCollPunt(16, O, m) 18, 19, 20, 21 … eveneens toegepast op de punten 11, 13, 14, 12 22. Kegelsnede(17, 18, 19, 20, 21) Beginobjecten: cirkel, O, m; eindobject: kegelsnede (in dit geval dus de hyperbool). |
8. Download ![]()
De meeste figuren van deze pagina, de figuren die gebruikt zijn bij de CabriJavapplets, en
de genoemde macro's zijn in ??n bestand te downloaden via deze website.
Klik hier om het downloadproces te starten
(ZIP-bestand, ca. 38Kb).
[genspiegel.htm] laatste wijziging op: 18-jan-18 (08-07-2001)