Morley's stelling (2)

Stelling van Morley [2]

Goniometrisch bewijs ][ Morley [1] | DK & Meetkunde

Een goniometrisch bewijs
De gedachte achter dit bewijs van de stelling van Morley bewijs is heel eenvoudig:

In de driehoeken ARB, BPC en CQA kennen we de bases - AB, BC, AC en de aanliggende hoeken. Met de sinusregel kunnen we dan de linstukken AR, BR, BP, CP, CQ en AQ berekenen.
Vervolgens passen we de cosinusregel toe op de driehoeken ARQ, BPR, CQP om de lijnstukken QR, PR, PQ te berekenen (en te vergelijken). Zijn ze aan elkaar gelijk, dan is de stelling bewezen

figuur 1

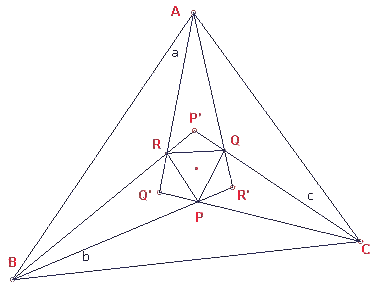Stel om een en ander iets te vereenvoudigen
?A = 3a, ?B = 3b, ?C = 3c.
Dit betekent dus, dat a + b + c = 60?. Voorts nemen we aan, dat de straal van de omgeschreven cirkel van driehoek ABC gelijk is aan ?.
De sinusregel geeft nu onmiddellijk
AB = sin(3c), BC =sin(3a) en AC = sin(3b).

Bekijk nu BPC. Wederom is nu, volgens de sinusregel,

BP/sin(c)

= BC/sin(180^o - b - c)
= sin(3a)/sin(b + c)
= sin(3a)/sin(60^o - a)

Daaruit vinden we
BP = sin(3a)sin(c)/sin(60^o - a).

Ten einde deze uitdrukking te vereenvoudigen, merken we op, dat

	sin(3a)	= 3sin(a) - 4sin³(a)
		= 4sin(a)[(?3 / 2)² - sin²(a)]
		= 4sin(a)[sin²(60^o) - sin²(a)]
		= 4sin(a)(sin(60^o) + sin(a))(sin(60^o) - sin(a))
		= 4sin(a) 2sin[(60^o) + a)/2]cos[(60^o) - a)/2] 2sin[(60^o) - a)/2]cos[(60^o) + a)/2]
		= 4sin(a)sin(60^o + a)sin(60^o - a)

Gebruiken we dit resultaat in de bovenstaande uitdrukking voor BP, dan is

BP = 4sin(a)sin(c)sin(60^o + a)

En op dezelfde manier

BR = 4sin(c)sin(a)sin(60^o + c)

Beide uitdrukkingen gebruiken we in de cosinusregel toegepast op driehoek:

PR² = BP² + BR² - 2 BP BR cos(b),

Waaruit we vinden

PR² = 16 sin²(a) sin²(c) [sin²(60^o + a) + sin²(60^o + c) - 2sin(60^o + a)sin(60^o + c)cos(b)]. (*)

Merk echter op, dat (60^o + a) + (60^o + c) + b = 180^o.
Dus is er een driehoek met hoeken (60^o + a), (60^o + c), and b.
Inderdaad, er bestaat een hele familie van driehoeken met deze hoeken (oa. en als voorbeeld a = 0, b = 60, c = 0 en ook a = 10, b = 45, c = 5).
Uit deze familie kiezen we de driehoek waarvan de straal van de omgeschreven cirkel ? is. Van deze driehoek hebben de zijden volgens de sinusregel (zoals hierboven) een eenvoudige vorm; opvolgend zijn de zijden gelijk aan sin(60^o + a), sin(60^o + c) en sin(b).
In deze driehoek passen we op de laatste zijde de cosinusregel toe:

sin²(b) = sin²(60^o + a) + sin²(60^o + c) - 2sin(60^o + a)sin(60^o + c)cos(b)

Waaruit volgt (zie de laatste factor tussen [ en ] in de uitdrukking van PR²; zie (*)):

PR = 4sin(a)sin(b)sin(c),

Deze uitdrukking is symmetrisch in a, b en c. QR en PQ zijn daardoor dus gelijk aan dezelfde uitdrukking als PR.
Dus PR = PQ = QR. ?

Hiermee is dus (en toch wel op elementaire wijze) de stelling van Morley opnieuw bewezen.

[morley2.htm] laatste wijziging op: 15-06-2000