In een cirkel beschreven driehoeken
1. Inleiding ![]()
We gaan uit van een cirkel K met middelpunt O en straal R.
H is een punt binnen de cirkel (dus 0 < |OH| < R).
We bewijzen:
| Stelling 1 Er zijn oneindig veel in de cirkel ingeschreven driehoeken die het punt H als hoogtepunt hebben. |
Bewijs:
| figuur 1a | 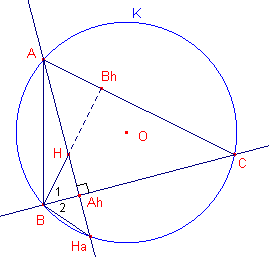 |
Een bekende eigenschap van het hoogtepunt van een driehoek ABC is, dat de
spiegelbeelden ervan in de zijden van de driehoek op de omgeschreven van de driehoek
liggen (zie bijvoorbeeld de pagina "De cirkel van
Feuerbach"). Zij nu A een willekeurig punt van de cirkel en m de lijn door A en H. m snijdt de cirkel voor de tweede keer in het punt Ha. De zijde BC van de driehoek is dan de middelloodlijn van het lijnstuk HHa. We moeten nu aantonen, dat H inderdaad het hoogtepunt van ABC is. We trekken de lijn BH,
die CA snijdt in Bh. Uit de constructie volgt nu dat � B1
= � B2. |
| figuur 1b | 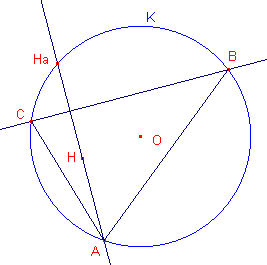 |
Opmerking |
Gevolg
Alle driehoeken hebben dezelfde negenpuntcirkel.
Immers de straal van de negenpuntcirkel is gelijk aan �R, terwijl het middelpunt ervan
alleen afhankelijk is van de punten O en H, namelijk het midden van OH (zie weer de pagina
"De cirkel van Feuerbach").
Klik hier ![]() voor een CabriJavapplet die het bovenstaande illustreert.
voor een CabriJavapplet die het bovenstaande illustreert.
2. Een ellips ![]()
In de hierbovenstaande CabriJavapplet werd reeds vermeld, dat de zijden
van de driehoek een ellips omhullen.
We zullen eea. hieronder bewijzen.
| Stelling 2 De zijden van een in een cirkel (met middelpunt O) beschreven driehoek ABC met binnen die cirkel gelegen hoogtepunt H raken aan een ellips die de negenpuntcirkel als hoofdcirkel heeft (brandpunten zijn O en H). |
Opmerking
Zie voor het begrip hoofdcirkel de pagina "Ellips-constructies met Cabri [2]".
[einde Opmerking]
| figuur 2 | 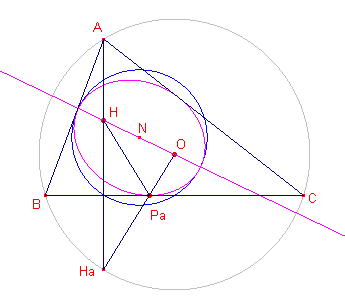 |
(zie figuur 2) De lijn OHa znijdt de lijn BC in het punt Pa.Nu is BC middelloodlijn van HHa, zodat PaH = PaHa. Nu volgt eenvoudig: PaO + PaH = PaO + PaHa = R (constant) Het punt Pa ligt dus op een ellips waarvan H en O de brandpunten zijn. N is het middelpunt van de cirkel met straal �R. De negenpuntcirkel is dus hoofdcirkel van deze ellips. De lijn BC deelt de buitenhoek tussen PaO en PaH middendoor, dus BC is raaklijn aan de ellips. Analoog bewijzen we raking voor de andere zijden van driehoek ABC. � |
Klik hier ![]() voor een CabriJavapplet die Stelling 2 illustreert.
voor een CabriJavapplet die Stelling 2 illustreert.
3. Download ![]()
De op deze pagina staande figuren, de figuren gebruikt in de CabriJavapplets en de
Cabri-macro Ellips1P2F.mac kunnen via deze
website in ��n bestand worden gedownload.
Klik hier om het downloadproces te
starten (ZIP-bestand; ca 5 kB)
[incirkdrieh.htm] laatste wijziging op: 17-06-02