Ellips: een meetkundige eigenschap

Overzicht  ][  Richtcirkel | Kegelsneden | Anal. meetkunde | Meetkunde

Zie ook

 de pagina "Ellips-constructies [4a]".

0. Overzicht begin pagina

  1. Inleiding
         Stelling 1 cabrisignal.gif (160 bytes)
  2. Meetkundig bewijs van Stelling 1
  3. Eigenschappen
         Stelling 2 cabrisignal.gif (160 bytes)
         Stelling 3
  4. Constructies
         Constructie 1: brandpunten, willekeurig punt, raaklijn, richtlijnen
         Constructie 2: richtlijnen
  5. Nog een eigenschap (van kegelsneden)
          Stelling 4 cabrisignal.gif (160 bytes)
  6. Constructies op basis van Stelling 4
         Constructie 3: richtlijn bij een brandpunt
         Constructie 4: brandpunt bij een richtlijn

1. Inleiding begin pagina
Op de pagina "Kegelsneden en hun vergelijkingen" vinden we in paragraaf 4.1:

Stelling 1 begin pagina
Een ellips is de meetkundige plaats van de punten X waarvoor de afstand tot een vast punt F (brandpunt) en de afstand tot een vaste rechte lijn r (richtlijn) een constante verhouding kleiner dan 1 hebben.
.
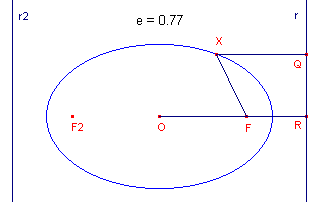figuur 1 richtlijn1.gif (1730 bytes) Nb.
In paragraaf 2 staat een meetkundig bewijs van Stelling 1.

In figuur 1 is   XF / XQ = e (de excentriciteit van de kegelsnede).
Vanwege de symmetrie van de ellips is er een tweede richtlijn (r2) behorende bij het brandpunt F2.
Uit de berekeningen op de pagina "Kegelsneden en hun vergelijking" volgde:
   OR = a2 /c
   e = c/a
waarbij a de lengte is van de halve hoofdas en OF = c.

Klik hier Animatie voor een CabriJavapplet bij het bovenstaande.

2. Meetkundig bewijs van Stelling 1 begin pagina

Gegeven : het getal e < 1, een richtlijn r1, een brandpunt F1 (zie figuur 2).
Te bewijzen :  de meetkundige plaats van de punten P met PF1/PQ = e is een ellips; hierbij is Q de projectie van P op r1.

Bewijs:

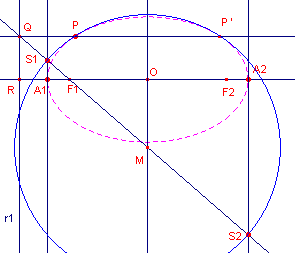figuur 2 richtlijn3.gif (3132 bytes) Op de as (de lijn door F1 loodrecht op r1) kunnen de punten A1 en A2 worden bepaald met A1F1/A2R = e en A2F1/A2R = e.
We kiezen nu F2 (op A1A2) zo, dat A2F2 = A1F1.
Zij P een punt met PF1/PQ = e.
Op de lijn PQ ligt nu een tweede punt P' met P'F1/P'Q = e.
De meetkundige plaats van de punten X waarvoor XF1 en XQ een constante verhouding hebben, is een Apollonius-cirkel (*) die door P en P' gaat.
Een middellijn van deze cirkel is het lijnstuk S1S2 waarbij
   S1F1 : S1Q = S2F2 : S2Q = e

Omdat ook A1R : A1F1 = A2R : A2F1 = e, zijn S1 en S2 de snijpunten van de lijn QF1 met de loodlijnen in A1 en A2 op de as.
Het middelpunt M van de Apollonius-cirkel is dan het midden van S1S2 (waarmee ook P' gevonden is).
Nu geldt:
   PF1/PQ1 = P'F1/P'Q = (PF1+P'F1)/(PQ + P'Q) = (PF1 + PF2)/2OR = e
waaruit we vinden
   PF1 + PF2 = 2e . OR
OR is constant; dus ook PF1 + PF2 = constant.
Het punt P ligt dus op een ellips met excentriciteit e. �
__________
(*)
Zie de pagina "Cirkels van Apollonius"

3. Eigenschappen begin pagina

Stelling 2 begin pagina
De loodlijnen in F1 en F2 op de brandpuntsvoerstralen van een punt P snijden de raaklijn in P in punten van de richtlijnen.

Klik hier Animatie voor een CabriJavapplet bij Stelling 2.

Bewijs: (zie figuur 3)]

� Klik hier voor een analytisch bewijs van Stelling 2. (Let op! Deze pagina is alleen leesbaar met MathPlayer)

figuur 3 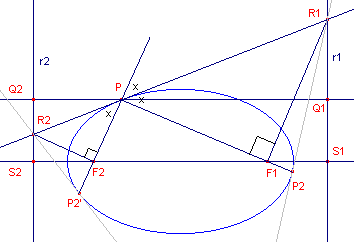richtlijn2.gif (3334 bytes) R1 en R2 zijn de snijpunten van de loodlijnen op de voerstralen met de raaklijn.
We zullen aantonen, dat de loodlijnen uit R i op de as de richtlijnen zijn van de ellips.
Uit het feit, dat de raaklijn gelijke hoeken maakt met de brandpuntvoerstralen volgt, dat driehoek PF2R2 gelijkvormig is met PF1R1, zodat
   PF1 : PF2 = PR1 : PR2 ......(1)
Q1 en Q2 zijn de voetpunten van P op de lijnen R iS i, zodat
   PQ1 : PQ2 = PR1 : PR2 ......(2)
Uit (1) en (2) volgt dan:

   PF1 : PF2 = PQ1 : PQ2
of
   (PF1+PF2) : PF1 = (PQ1 + PQ2) : PQ1
of ook
   PF1/PQ1 = (PF1+PF2)/(PQ1+PQ2) = 2a / (PQ1 + PQ2) = c/a
Uit dit laatste volgt:
   PQ1 + PQ2 = 2a2/c
zodat S1S2 = 2a2/c. R1S1 en R2S2 zijn dus de richtlijnen van de ellips (zie Inleiding). �

Gevolg
De raaklijnen in P2 (snijpunt van PF1) en in P2' (snijpunt van PF2) gaan door opvolgend R1 en R2 (zie figuur 3 en bovenstaande CabriJavapplet).
Immers ook voor deze punten staan F1R1 en F2R2 loodrecht op de voerstralen.

Definitie
De raakkoorde van een punt is de verbindingslijn van de raakpunten van de raaklijnen uit dat punt.

Uit het bewijs van Stelling 2 volgt dan direct

Stelling 3a begin pagina
De raakkoorden van een punt van de richtlijn gaat door het bijbehorende brandpunt
of, anders geformuleerd
De meetkundige plaats van de punten waarvan de raakkoorden door een brandpunt gaan, is de bijbehorende richtlijn.

Op basis van de begrippen pool en poollijn (zie daarvoor de pagina "Pooltransformatie") kunnen we ook formuleren:

Stelling 3b begin pagina
Een richtlijn is de poollijn van het bijbehorende brandpunt.

[einde Gevolg]

4. Constructies begin pagina
Op basis van het voorgaande kunnen we nu een aantal constructies uitvoeren, bij gegeven hoofdas en nevenas.

[1] Constructie van, in deze volgorde (zie figuur 4): begin pagina
         (1.1) brandpunten
         (1.2) een willekeurig punt P
         (1.3) raaklijn in P
         (1.4) richtlijnen.

figuur 4 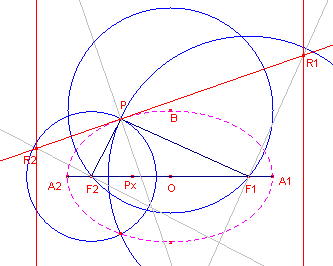richtlijn4.gif (4316 bytes) (1.1)
De cirkel(B, OA1) snijdt het lijnstuk A1A2 in F1 en F2, immers BF1 = BF2 = a.
(1.2)
Px ligt op A1A2. Dus PxA1 + PxA2 = 2a
De cirkels (F1,PxA1) en (F2,PxA2) snijden elkaar in punten P van de ellips.
(1.3)
De raaklijn is bissectrice van de nevenhoek van hoek F1PF2.
(1.4)
De richtlijnen zijn de loodlijnen uit R1 en R2 op de hoofdas. R1 en R2 zijn gevonden op basis van Stelling 2 (loodlijnen op de voerstralen).

[2] Constructie van de richtlijnen, bij gegeven hoofdas en brandpunten begin pagina

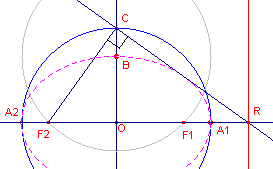figuur 5 richtlijn5.gif (2339 bytes) OC = a
CR loodrecht op CF2 in punt C.
Nu is in driehoek CF2R: CO2 = OF2 . OR.
Dus OR = a2/c.

5. Nog een eigenschap (van kegelsneden) begin pagina

Stelling 4 begin pagina
Een koorde P1P2 van een ellips (kegelsnede) snijdt een richtlijn r (bij brandpunt F) in een punt S, en wel zo, dat SF gelijke hoeken maakt de voerstralen FP1 en FP2.

Bewijs: (zie figuur 6)

figuur 6 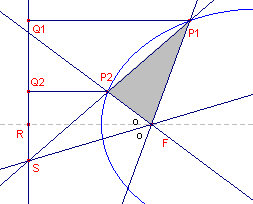richtlijn6.gif (2170 bytes) Q1 en Q2 zijn de voetpunten van P1 en P2 op r.
Nu geldt:
   P1F/P1Q1 = P2F/P2Q2 = e waaruit volgt
   P1Q1/P2Q2 = P1F/P2F ......(1)
Maar ook hebben we (in driehoek SP1Q1):
   P1Q1/P2Q2 = P1S/P2S ......(2)
Uit (1) en (2) volgt:
   P1F/P2F = P1S/P2S
Volgens de buitenbissectricestelling is dan FS een buitenbssectrice van driehoek FP1P2. �

Klik hier Animatievoor een CabriJavapplet bij Stelling 4 (ellips en hyperbool).
Klik hier Animatievoor een CabriJavapplet bij Stelling 4 (parabool).

6. Constructies op basis van Stelling 4 begin pagina

[3] begin pagina

Gegeven : punten P1, P2, P3 van een kegelsnede en een brandpunt F
Te construeren : de richtlijn bij F

Constructie :

figuur 7 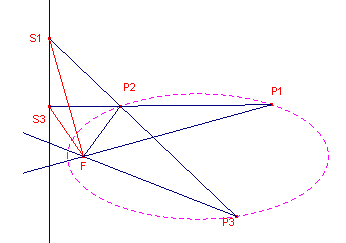richtlijn7.gif (2113 bytes) S1 wordt gevonden als snijpunt van P2P3 en de bissectrice van de buitenhoek bij F van driehoek FP2P3.
S3 wordt gevonden als snijpunt van P1P2 en de bissectrice van de buitenhoek bij F van driehoek FP1P2.
De gevraagde richtlijn is de lijn S1S3.

[4] begin pagina

Gegeven : punten P1, P2, P3 van een kegelsnede en een richtlijn
Te construeren : het brandpunt F bij de richtlijn

Constructie :

figuur 8 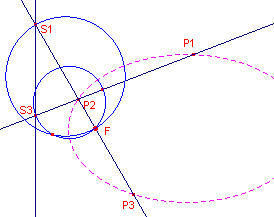richtlijn8.gif (2110 bytes) We bepalen het punt F als snijpunt van twee Apollonius-cirkels.
De ene cirkel is die op P1P2 die door S3 gaat (S3 is het snijpunt van de richtlijn met de lijn P1P2).
De tweede cirkel is de Apollonius-cirkel op P2P3 die door S1 gaat.
Een van de snijpunten van de cirkels is dan het gevraagde brandpunt.

Nb.
Er voldoen in het algemeen dus twee kegelsneden. We vinden immers twee brandpunten bij dezelfde richtlijn. In dit geval is de tweede kegelsnede een hyperbool.

Opmerking
Voor de constructie van de Apollonius-cirkels zie de pagina "Cirkels van Apollonius".
[einde Opmerking]

begin pagina
[richtlijn.htm] laatste wijziging op: 23-06-04