Een meetkundige eigenschap van een ellips
Stelling
De loodlijnen in F1 en F2 op de brandpuntsvoerstralen van een punt P van een ellips
snijden de raaklijn in P in punten van de richtlijnen.
Bewijs:
|
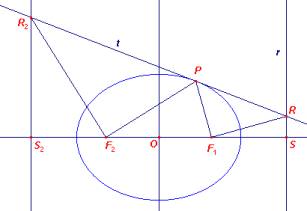
|
We tonen de stelling aan
met behulp van de vergelijking van de ellips (analytisch).
We gaan uit van de ellips
met vergelijking:
x
2
a
2
+
y
2
b
2
=1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bm0BWLhiVzgicXwyJTgapeWaaSaaaeaacaWG4bWaaWbaaSqabeaacaqGYaaaaaGcbaGaamyyamaaCaaaleqabaGaaGOmaaaaaaGccqGHRaWkdaWcaaqaaiaadMhadaahaaWcbeqaaiaaikdaaaaakeaacaWGIbWaaWbaaSqabeaacaaIYaaaaaaakiabg2da9iaaigdaaaa@45E4@
Stel de coördinaten van P
zijn: (x0, y0).
De raaklijn t in P
aan de ellips heeft dan de vergelijking:
t:
x
0
x
a
2
+
y
0
y
b
2
=1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bm0BWLhiVzgicXwyJTgapeGaamiDaiaacQdacaaMe8UaaGjbVlaaysW7daWcaaqaaiaadIhadaWgaaWcbaGaaGimaaqabaGccaWG4baabaGaamyyamaaCaaaleqabaGaaGOmaaaaaaGccqGHRaWkdaWcaaqaaiaadMhadaWgaaWcbaGaaGimaaqabaGccaWG5baabaGaamOyamaaCaaaleqabaGaaGOmaaaaaaGccqGH9aqpcaaIXaaaaa@4E3F@
|
We bekijken de situatie
voor het brandpunt F1 = (c, 0). Een vergelijking van
de bij dat punt behorende richtlijn r is:
r: x=
a
2
c
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bieB1v2vLj2uPrxza8qacaWGYbGaaiOoaiaaysW7caaMe8UaaGjbVlaadIhacqGH9aqpdaWcaaqaaiaadggadaahaaWcbeqaaiaaikdaaaaakeaacaWGJbaaaaaa@4673@
Voor de coördinaten
(x,y)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhacaGGSaGaamyEaiaacMcaaaa@39F2@
van het snijpunt R van t en r
hebben we dan
R: {
x=
a
2
c
x
0
x
a
2
+
y
0
y
b
2
=1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bieB1v2vLj2uPrxza8qacaWGsbGaaiOoaiaaysW7caaMe8UaaGjbVpaaceaabaqbaeaabiqaaaqaaiaadIhacqGH9aqpdaWcaaqaaiaadggadaahaaWcbeqaaiaaikdaaaaakeaacaWGJbaaaaqaamaalaaabaGaamiEamaaBaaaleaacaaIWaaabeaakiaadIhaaeaacaWGHbWaaWbaaSqabeaacaaIYaaaaaaakiabgUcaRmaalaaabaGaamyEamaaBaaaleaacaaIWaaabeaakiaadMhaaeaacaWGIbWaaWbaaSqabeaacaaIYaaaaaaakiabg2da9iaaigdaaaaacaGL7baaaaa@53C4@
Eliminatie van x
hieruit levert:
x
0
a
2
c
a
2
+
y
0
y
b
2
=1 ⇒
x
0
c
+
y
0
b
2
y=1 ⇒ y=
b
2
y
0
(1−
x
0
c
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bieB1v2vLj2uPrxza8qadaWcaaqaaiaadIhadaWgaaWcbaGaaGimaaqabaGcdaWcaaqaaiaadggadaahaaWcbeqaaiaaikdaaaaakeaacaWGJbaaaaqaaiaadggadaahaaWcbeqaaiaaikdaaaaaaOGaey4kaSYaaSaaaeaacaWG5bWaaSbaaSqaaiaaicdaaeqaaOGaamyEaaqaaiaadkgadaahaaWcbeqaaiaaikdaaaaaaOGaeyypa0JaaGymaiaaysW7caaMe8UaaGjbVlabgkDiElaaysW7caaMe8UaaGjbVpaalaaabaGaamiEamaaBaaaleaacaaIWaaabeaaaOqaaiaadogaaaGaey4kaSYaaSaaaeaacaWG5bWaaSbaaSqaaiaaicdaaeqaaaGcbaGaamOyamaaCaaaleqabaGaaGOmaaaaaaGccaWG5bGaeyypa0JaaGymaiaaysW7caaMe8UaaGjbVlabgkDiElaaysW7caaMe8UaaGjbVlaadMhacqGH9aqpdaWcaaqaaiaadkgadaahaaWcbeqaaiaaikdaaaaakeaacaWG5bWaaSbaaSqaaiaaicdaaeqaaaaakiaacIcacaaIXaGaeyOeI0YaaSaaaeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaaGcbaGaam4yaaaacaGGPaaaaa@76D9@
De coördinaten van R
zijn dan:
R=(
a
2
c
;
b
2
y
0
(1−
x
0
c
)
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bieB1v2vLj2uPrxza8qacaWGsbGaeyypa0ZaaeWaaeaadaWcaaqaaiaadggadaahaaWcbeqaaiaaikdaaaaakeaacaWGJbaaaiaacUdadaWcaaqaaiaadkgadaahaaWcbeqaaiaaikdaaaaakeaacaWG5bWaaSbaaSqaaiaaicdaaeqaaaaakiaacIcacaaIXaGaeyOeI0YaaSaaaeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaaGcbaGaam4yaaaacaGGPaaacaGLOaGaayzkaaaaaa@4BF7@
We hebben nu als
richtingscoëfficiënten rc(F1R) en rc(F1P)
van de lijnen F1R en F1P
opvolgend:
rc(
F
1
R)=
b
2
y
0
(1−
x
0
c
)−0
a
2
c
−c
=
b
2
y
0
(c−
x
0
)
a
2
−
c
2
=
b
2
(c−
x
0
)
b
2
y
0
=
c−
x
0
y
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bieB1v2vLj2uPrxza8qacaWGYbGaam4yaiaacIcacaWGgbWaaSbaaSqaaiaaigdaaeqaaOGaamOuaiaacMcacqGH9aqpdaWcaaqaamaalaaabaGaamOyamaaCaaaleqabaGaaGOmaaaaaOqaaiaadMhadaWgaaWcbaGaaGimaaqabaaaaOGaaiikaiaaigdacqGHsisldaWcaaqaaiaadIhadaWgaaWcbaGaaGimaaqabaaakeaacaWGJbaaaiaacMcacqGHsislcaaIWaaabaWaaSaaaeaacaWGHbWaaWbaaSqabeaacaaIYaaaaaGcbaGaam4yaaaacqGHsislcaWGJbaaaiabg2da9maalaaabaWaaSaaaeaacaWGIbWaaWbaaSqabeaacaaIYaaaaaGcbaGaamyEamaaBaaaleaacaaIWaaabeaaaaGccaGGOaGaam4yaiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaGccaGGPaaabaGaamyyamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaadogadaahaaWcbeqaaiaaikdaaaaaaOGaeyypa0ZaaSaaaeaacaWGIbWaaWbaaSqabeaacaaIYaaaaOGaaiikaiaadogacqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaaqaaiaadkgadaahaaWcbeqaaiaaikdaaaGccaWG5bWaaSbaaSqaaiaaicdaaeqaaaaakiabg2da9maalaaabaGaam4yaiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaaakeaacaWG5bWaaSbaaSqaaiaaicdaaeqaaaaaaaa@7367@
rc(
F
1
P)=
y
0
−0
x
0
−c
=
y
0
x
0
−c
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bieB1v2vLj2uPrxza8qacaWGYbGaam4yaiaacIcacaWGgbWaaSbaaSqaaiaaigdaaeqaaOGaamiuaiaacMcacqGH9aqpdaWcaaqaaiaadMhadaWgaaWcbaGaaGimaaqabaGccqGHsislcaaIWaaabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaadogaaaGaeyypa0ZaaSaaaeaacaWG5bWaaSbaaSqaaiaaicdaaeqaaaGcbaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaadogaaaaaaa@503F@
Uit beide laatste
uitdrukkingen volgt nu eenvoudig:
rc(
F
1
R)⋅rc(
F
1
P)=−1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeeaaaaaq9bieB1v2vLj2uPrxza8qacaWGYbGaam4yaiaacIcacaWGgbWaaSbaaSqaaiaaigdaaeqaaOGaamOuaiaacMcacqGHflY1caWGYbGaam4yaiaacIcacaWGgbWaaSbaaSqaaiaaigdaaeqaaOGaamiuaiaacMcacqGH9aqpcqGHsislcaaIXaaaaa@4BCF@
waaruit blijkt, dat de
lijnen F1R en F1P loodrecht
op elkaar staan.
