[1]
Voor elke re�el getal x bestaat er een re�el getal t waarvoor x = [x] + t met 0 � t < 1.
t heet het fractionele deel van x.
[2]
Uit a =qb + r met 0 � r < |b| volgt dan
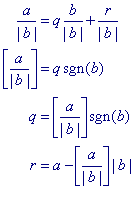
[einde Gevolgen]
Definities | Algoritmen | Priemgetallen | Hoofdstelling | Functie van Euler ][ Getallentheorie
Zie ook pagina "Mersenne-priemgetallen"
Zie ook pagina "Bronnen en
informatie over priemgetallen"
| Definitie Een geheel getal a heet een deler van het getal b, als er een geheel getal k bestaat, zodat ak = b. Schrijfwijze: a | b. Het getal b heet dan ook wel een veelvoud van het getal a. |
Gevolgen
[1] Elk getal is deler van het getal 0, terwijl 0 geen deler is van een
van 0 verschillend getal.
[2] Uit a | b volgt (-a) | b, a | (-b) en (-a)
| (-b).
[3] a | a en 1 | a.
[4] Uit a | b en b | c volgt a | c
Immers
Er zijn getallen k1 en k2 met ak1 = b
en bk2 = c, zodat ak1k2
= bk2 = c.
[einde Gevolgen]
| Stelling 1 De enige delers van 1 zijn +1 en -1. |
Bewijs:
Uit |ab |= |a|.|b| = 1 waarbij a=0 en b=0
uitgesloten zijn, volgt |a| � 1, |b|
� 1
Zou nu gelden |a| > 1, dan is |a|.|b| �
1. Dus is |a| = 1.
Evenzo geldt dan ook |b| = 1.
Waaruit dus volgt dat a = � 1 en b = � 1. �
| Definities [1] Een deler d van a heet echte deler van het getal a als d � �1 en d � �a. [2] Een geheel getal dat groter is dan 1 en geen echte delers heeft, heet ondeelbaar getal of priemgetal. |
De rij priemgetallen is dus:
2, 3, 5, 7, 11, 13, 17, 19, 23, ...
Voor priemgetallen zie verder paragraaf 3.
Overzicht
2.1.1. Het bewijs van de delingsalgoritme
| Stelling 2 - delingsalgoritme Zijn a en b (met b � 0) gehele getallen, dan zijn er unieke getallen q en r zodanig, dat a = qb + r waarbij 0 � r < |b| |
Bewijs:
Zij A de verzameling van de getallen van de vorm a - xb, waarbij
x een geheel getal is.
Zij S de verzameling van de (niet-negatieve) getallen in A.
Nu is S een deelverzameling van de niet-negatieve getallen.
Voorbeeld
x = -|a|sgn(b) geeft in A het getal a + |a|.|b|,
en dit getal is niet-negatief, omdat |b| � 1.
Nb.
sgn(x) is de "teken-functie": sgn(x) = 1 als x positief is;
sgn(x) = -1 als x negatief is; sgn(x) = 0 als x = 0
[einde Nb en einde Voorbeeld]
S heeft een kleinste element r.
Zij nu r bepaald door x = q, dan is a - qb = r.
Dus:
a = qb + r
We bewijzen nu het tweede deel van de stelling.
Zij r � |b| > 0
(veronderstelling).
Dan is 0 � r - |b| < r
en r - |b| = a - qb - |b| = a - ( q + sgn(b) )b.
Het getal r - |b| behoort dus tot S, maar het is kleiner dan r.
Tegenspraak. Dus
0 � r < |b|
Het bestaan van q en r is nu dus aangetoond.
We bewijzen tenslotte de uniciteit van q en r.
Zij a = qb + r en a = q1b + r1
met 0 � r < |b| en 0
� r1 < |b|
(veronderstelling).
Hieruit vinden we
0 � | r - r1|
< |b|
maar ook geldt
| r - r1| =
| q - q1|.|b|
Tegenspraak. Dus q en r zijn uniek. �
Opmerking
De gebruikelijke algoritme voor de deling van twee
positieve getallen levert het getal r, dat de hoofdrest
van de deling wordt genoemd.
Immers
7 / 128 \ 18
7
58
56
2
Nu is 128 = 18 . 7 + 2. Hierbij is dus q = 18 en r =
2.
Bij deling van een negatief getal is dat echter niet zo:
-128 = (-19) . 7 - 2
De hoofdrest vinden we hier via -128 = (-19) . 7 + 5. Nu is q
= -19 en r = 5.
Zie paragraaf 2.1.2. De Entier-functie
voor een verdere uitwerking hiervan.
[einde Opmerking]
| Definitie De functie f(x) = [x] heet de Entier-functie. [x] wordt daarbij vastgelegd als het gehele getal n met n � x < n + 1. [x] is dus het grootste gehele getal kleiner dan of gelijk aan x. We spreken [x] uit als "entier van x". We schrijven soms ook wel E(x) in plaats van [x]. |
Gevolgen
[1]
Voor elke re�el getal x bestaat er een re�el getal t
waarvoor x = [x] + t met 0 �
t < 1.
t heet het fractionele deel van x.
[2]
Uit a =qb + r met 0 � r
< |b| volgt dan
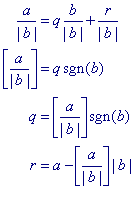
[einde Gevolgen]
2.2.1 Kleinste gemene veelvoud
| Definitie V(a1, a2, ..., an) is de verzameling van alle getallen die deelbaar zijn door elke ai (ai � 0).. De getallen van V heten de gemeenschappelijke veelvouden van a1, a2, ..., an. |
| Stelling 3 De verzameling V+ van positieve getallen uit V is niet leeg. |
Bewijs:
Het productl |a1a2a3...an|
is element van V+.�
Gevolg
V+ heeft een kleinste element.
Dit kleinste element van V+ speelt een bijzondere rol (als kgv)
in hetgeen volgt
[einde Gevolg]
| Definitie Het kleinste element van V+(a1,..., an) heet kleinste gemeenschappelijke veelvoud (kgv) van a1, a2, ..., an. De functie die a1, a2, ..., an op het kgv daarvan afbeeldt, geven we aan met kgv(a1,a2, ..., an). |
| Stelling 4 Als m = kgv(a1, ..., an) dan een getal l is element van V(a1, a2, ..., an) DESDA m | l. |
Bewijs:
[1] m | l houdt in, dat l deelbaar is door iedere ai
(volgens de definitie van m).
Daarom is l een gemeenschappelijk veelvoud van a1,
..., an. Dus l is element van V.
[2] l een element van V.
Volgens Stelling 2 is nu voor l en m
: l = qm + r, waarbij 0 � r < m
Nu geldt: m in V, dus qm in V, l in V, dus
ook r = l - qm in V+; immers r �
0).
Wegens r < m, terwijl m de kleinste van V+
is, moet dus gelden: r = 0.
Dus l = qm, zodat m | l.�
| Definitie D(a1, a2, ..., an) is de verzameling van alle gemeenschappelijke delers van de getallen a1, a2, ..., an. |
| Stelling 5 De verzameling D+ van alle positieve elementen uit D is niet-leeg en eindig. |
Bewijs:
1 is deelbaar op elke ai. D+ is dus niet-leeg.
Het aantal delers van elke ai is eindig. D+ is de
doorsnede van een aantal eindige verzamelingen. Dus is D+
eveneens eindig.�
Gevolg
De verzameling D+ heeft een grootste element.
Dit grootste element van D+ speelt een bijzondere rol (als ggd)
in hetgeen volgt.
[einde Gevolg]
| Definitie Het grootste element van D+ heet grootste gemeenschappelijke deler (ggd) van de getallen a1, a2, ..., an. De functie die a1, a2, ..., an afbeeldt op de ggd daarvan, geven we aan met ggd(a1, a2, ..., an). Indien er geen verwarring kan ontstaan schrijven ook wel (a1, a2, ..., an). |
| Stelling 6 Als d = ggd(a1, a2, ..., an), dan zijn er gehele getallen xi, zodat d = x1a1 + x2a2 + ... + xnan |
Bewijs:
Zij, bij gegeven getallen a1, a2, ..., an,
S de verzameling van alle getallen a van de vorm
a = a1x1 + a2x2
+ ... +anxn
De verzameling S is niet-leeg, immers S bevat |a1|, met x1
= sgn(a1), x2=x3=...=xn=0
De verzameling positieve getallen in S heeft dus een kleinste; stel d0
is die kleinste.
Volgens Stelling 2 (delingsalgoritme) is er nu bij elke
element m van S een q en een r zodat
m = d0q + r met r <d0
Uit
r = m - d0q
m = a1x1 + ... + anxn
d0 = a1y1 + ... + anyn
leiden we nu af:
r = a1(x1 - qy1) + ...
+an(xn - qyn)
Dus r behoort eveneens tot S. Maar d0 is het kleinste positieve
getal, dus r = 0.
We vinden dus d0 | m.
Daar m willekeurig is in S, is d0 dus eveneens
deler van ai (immers ai is element van S (xj = 0
en xi <> 0)
Volgens de definitie van d is nu
d0 � d.
Uit d | ai volgt d | d0, zodat dus ook
d � d0
Met andere woorden: d = d0, waaruit de stelling volgt.�
| Stelling 7 [1] Als d = ggd(a1, ...an) dan een geheel getal d1 is gemeenschappelijke deler van a1, ..., an DESDA d1 | d [2] Als voor a1, ..., an (gehele getallen ongelijk aan 0) geldt dat d1 = a1, d2 = (d1, a2), d3 = (d2, a3), ..., dn = (dn-1, an), dan dn = ggd(a1, a2, ..., an). |
Bewijs:
[1]
Als d1 | d, dan is, omdat d = ggd(a1, ..., an),
d1 | ai. Dus d1 is gemeenschappelijke
deler van ai.
Stel nu dat d1 gemeenschappelijke deler is van ai.
Volgens Stelling 6 zijn er dan getallen xi
met d = a1x1 + ... + anxn. Dus
d1 | d. �
[2]
We bewijzen met inductie.
De stelling is juist voor n = 2, immers d2= (d1, a2)
= (d1, a2).
Stel nu dn = ggd(a1, ..., an) , inductie-veronderstelling.
Zij verder en+1 = ggd(a1, ..., an, an+1).
Omdat en+1 deelbaar is op a1, ..., an+1,
is en+1 ook deelbaar op a1, ...,an.
Volgens Stelling 7.1 hebben we dan: en+1 | dn.
Hieruit concluderen we dan en+1 | ggd(dn, an+1);
dat wil zeggen en+1 | dn+1.
Maar er geldt ook
dn+1 | dn en dn+1 | an+1
Gebruiken we weer Stelling 7.1, dan zien we dat dn+1
| ai (met i = 1, 2, ..., n+1), zodat dan
dn+1 | en+1
Dus dn+1 = ggd(a1, a2, ..., an+1)
Waarmee door inductie stelling 7.2 bewezen is. �
In het bovenstaande hebben we nog steeds geen methode aangegeven om ggd(a1,
..., an) te vinden.
Stelling 7.2 toont echter aan, dat het voldoende is de
ggd van telkens twee van die getallen te bepalen.
In paragraaf 2.3 wordt een methode (de Euclidische
algoritme) behandeld waarmee dit gedaan kan worden.
| Stelling 8 - Euclidische
algoritme Het voortgezette delingsproces van twee getallen a1, a2 (gebaseerd op Stelling 2 en hieronder verder beschreven) breekt na een eindig aantal stappen af en levert ggd(a1, a2) |
Bewijs:
We gaan (zonder de algemeenheid geweld aan te doen) uit van de positieve
getallen a1 en a2 (waarbij a2 �
a1).
Volgens Stelling 2 zijn er dan getallen q1
en a3 zodat
a1 = a2q1 + a3
met a3 < a2
Als a3 = 0, dan a2 | a1, en dus a2
= ggd(a1, a2)
Als a3 > 0, dan zijn er (weer volgens Stelling
2) getallen q2 en a4 zodat
a2 = a3q2 + a4
met a4 < a3
Op deze manier doorgaande vinden we de rij getallen
a1 > a2 > a3 > a4
> ...
Deze rij van niet-negatieve getallen moet na een eindig aantal stappen
afbreken.
Stel dat dit het geval is na r - 1 stappen. Dan is dus
ar � 0 en ar+1 = 0
De laatste twee stappen zijn dan
ar-2 = ar-1qr-2 + ar
met 0 < ar < ar-1 < .. .< a1
ar-1 = arqr-1
Nu is ar = ggd(a1, a2), immers:
Het proces teruglezend, zien we dat
ar | ar-1, ar | ar-2,
..., ar | a2, ar | a1
Dus
ar | ggd(a1, a2)
Maar ook, lezend vanaf het begin van het proces:
(a1, a2) | a3, (a1,
a2) | a4 , ..., (a1, a2) | ar
Dus ar = ggd(a1, a2). �
Voorbeeld
We tonen aan, dat ggd(1147, 851) = 37
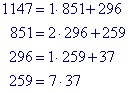
Dus ggd(1147, 851) = 37.
Uit het proces vinden we ook
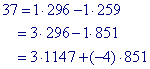
De getallen x1 en x2, als bedoeld in Stelling
6, zijn dus x1 = 3, x2 = -4.
[einde Voorbeeld]
Opmerking
Een toepassing van de Euclidische algoritme is te vinden op de pagina "Kettingbreuken".
[einde Opmerking]
| Stelling 9 Als a, b, k gehele getallen zij, dan geldt ggd(a, b) = ggd(a + kb, b). |
Bewijs:
Zij d = (a,b) en d1 = (a + kb, b).
Dus is d | a en d | b, dus d | (a + kb), dus eveneens d | d1.
Maar ook d1 | (a + kb) en d1 | b. Daaruit volgt, dat
d1 | (a + kb - kb), zodat d1 | a.
Uit d1 | a en d1 | b volgt dan d1 | d
Zodat d = d1.�
Opmerking
We kunnen natuurlijk ook zeggen
ggd(a,b) = ggd(a - kb, b) = ggd(b, a - kb)
Gevolg
Op basis hiervan kunnen we op eenvoudige wijze een recursieve functie
definieren die de ggd van twee getallen a en b berekent.
Als 1e voorbeeld in een programmeertaal (in dit geval UniComal)
FUNC ggd(a,b) CLOSED //
IF a MOD b=0 THEN
// a MOD b=0 betekent: a heeft rest 0 bij deling door b
RETURN b
ELSE
RETURN ggd(b,a MOD b)
ENDIF
ENDFUNC ggd
De opdracht
PRINT ggd(1147, 851)
geeft als resultaat
37
Zie ook de pagina "UniComal".
Een tweede voorbeeld staat in een Maple-worksheet (merk op, dat de beschrijvung van de procedure ggd hierin veel overeenkomst vertoont met de hierboven staande FUNCtie).
> restart: > ggd:=proc(a,b) > if a mod b = 0 then > RETURN (b) > else > RETURN (ggd(b, a mod b)) > fi > end:> ggd(1147, 851);
37
Zie voor andere Maple-worksheets de pagina "Maple
V".
[einde Opmerking en einde Gevolg]
3. Priemgetallen
Klik hier voor de definitie van
priemgetal.
| Definitie Een deler van een getal n die priem is, heet priemdeler van dat getal. |
| Stelling 10 Elk getal groter dan 1 heeft tenminste ��n priemdeler. |
Bewijs:
Zij d de kleinste positieve deler van van n (maar wel
groter dan 1).
Dan is d een priemgetal.
Stel dat dit niet zo is (veronderstelling), dan is d = d1d2
met 1 < di < d
Nu is bijvoorbeeld d1 ook een deler van n,
maar dit is in strijd met de definitie van d (als kleinste
deler).
Dus de veronderstelling is onjuist. �
| Stelling 11 Er zijn oneindig veel priemgetallen. |
Bewijs:
We laten hieronder het bewijs volgen, zoals dat door Euclides
(Euclides van Alexandri�, ~325 - ~265 vC) is
gegeven als Propositie 20 van Boek IX van zijn Elementen.
Uiteraard bewijst Euclides deze stelling door gebruik te maken van
lijnstukken die de getallen representeren. We zullen dat hier echter
achterwege laten.
Zijn A, B, C priemgetallen.
Ik zeg nu dat er meer priemgetallen zijn dan A, B en C.
Zij D het kleinste getal, dat gemeten wordt door A,B,C. [dk: d = abc].
Laat de eenheid nu bij D worden opgeteld tot F [dk: we bekijken dus f =
d+1 = abc +1]
Nu is F een priemgetal of niet.
Ten eerste, zij F een priemgetal; dan hebben we de priemgetallen A,B,C,F;
en dat zijn er meer dan A,B,C.
Vervolgens, zij F geen priemgetal; dan moet het gemeten worden [dk:
deelbaar zijn] door een priemgetal.
Laat het gemeten worden door het primegetal G.
Ik zeg nu, dat G niet hetzelfde is als de getallen A,B,C.
Maar we gaan ervan uit dat dit wel zo is.
A,B,C meten D; G meet D dus eveneens. Maar het [dk: G] meet ook F. G moet
dus ook de eenheid meten. En dit is onzin.
Dus G valt niet samen met A,B,C; en volgens de veronderstelling is het een
priemgetal.
Dus hebben we de priemgetallen A,B,C,G gevonden; en dat zijn er meer dan
A,B,C.
Hetgeen bewezen moest worden. �
4. Hoofdstelling van de rekenkunde
| Stelling 12 Elk geheel getal n > 1 kan worden geschreven als een product van priemgetallen. |
Bewijs:
We gebruiken inductie.
De stelling is juist voor het getal 2.
(Inductie-veronderstelling) Stel de stelling is bewezen voor 2, 3 , 4, 5,
6 ..., n.
Beschouw nu het getal n+1.
Als n+1 een priemgetal is, dan is het gestelde juist.
Als n+1 geen priemgetal is, dan geldt n+1 = n1n2
(met 1 < ni < n).
Volgens de inductie-veronderstelling kunnen n1 en n2
elk geschreven worden als een product van priemgetallen
Dus n+1 kan ook geschreven worden als een product van priemgetallen.
Het gestelde volgt nu via inductie. �
Voordat we een zeer belangrijke stelling uit de Getallentheorie (de hoofdstelling van de rekenkunde) geven, bewijzen we eerst een
| Hulpstelling 13 [1] Als p een priemgetal is met p | mn, dan p | m of p | n. [2] Als p, p1, p2, p3, ..., pn priemgetallen zijn met p | (p1p2p3...pn), dan p = pi voor zekere i (1 � i � n). |
Bewijs:
[1]
Stel p is niet deelbaar op m. Dan is dus ggd(p,m) = 1. Volgens Stelling
6 zijn er dan getallen x en y, met
px + my = 1
Dus geldt ook
pxn + myn = n
Omdat p | mn, is er een getal k, zodat pk = mn. Uit de relatie in de
vorige regel volgt dan
n = pxn + pky = p (xn + ky).
En hieruit volgt p | n. �
[2]
Uit Hulpstelling 13.1 volgt nu onmiddellijk p | p1
of p | (p2...pn).
Als p niet deelbaar is op p1, dan geldt weer volgens Hulpstelling
13.1 : p | p2 of p | (p3...pn).
Dus met een eindig aantal toepassingen van Hulpstelling
13.1 vinden we dat p | pi voor zekere i.
Omdat p en pi priem zijn, geldt p = pi. �
| Stelling 14 - hoofdstelling
van de rekenkunde Een geheel getal kan slechts op ��n manier geschreven worden als een product van priemgetallen (op de volgorde van de factoren na). |
Bewijs:
Stel dat
n = p1p2...pr = q1q2...qs
waarin p1, p2, ..., pr, q1, q2,
..., qs priemgetallen zijn.
Stel ook dat deze getallen in de representatie van n niet-dalend
geordend zijn.
We zullen nu aantonen, dat r = s en dat pi = qi.
We gebruiken inductie.
Het gestelde is juist voor n = 2.
Stel de bewering is juist voor 2, 3, 4, 5, ..., n-1
(inductie-veronderstelling).
Beschouw nu het getal n.
Als n priem is, dan is de stelling juist.
Als n niet-prime is, dan hebben we r > 1 en s > 1.
Volgens Hulpstelling 13.2 geldt nu q1 = pi
(voor zekere i) en p1 = q j (voor zekere j).
Omdat nu (vanwege de ordening) p1 �
pi = q1 � q j
= p1, vinden we (insluitend): p1 = q1.
Voor het gehele getal n / p1 (met 1 < n/p1 <
n) geldt dan de schrijfwijze
n/p1 = p2...pr = q2...qs
Uit de inductie-veronderstelling volgt dan dat r = s en pi = q i
(voor i = 2, ..., r)
Dus ook r = s en pi = q i (voor i = 1, ..., r).
Het gestelde volgt dus via inductie. �
Opmerkingen
[1] Uit Stelling 14 volgt dat een
geheel getal n geschreven kan worden als
| n = |
waarin de getallen pi primegetallen zijn met p1
< p2 < ...< pr met positieve gehele
exponenten ai.
Deze uitdrukking heet wel de priemrepresentatie van n.
Als we de rij priemgetallen schrijven als p1, p2,
... , dan is
| n = |
waarin een eindig aantal exponenten ai ongelijk aan 0 is.
[2] Een willekeurig geheel getal n kan nu worden geschreven als
| n = � |
waarbij we het + teken gebruiken als n positief is, en het - teken als n negatief is.
[3] Als n een rationaal getal is (ongelijk aan 0 en ongelijk aan �1), dan kan n geschreven worden als
| n = � |
waarin de exponenten ai positief
of negatief zijn.
[einde Opmerkingen]
5. Functie van Euler (indicator
van
Euler)
We zullen in deze paragraaf iets zeggen over het aantal getallen dat relatief
priem is met een gegeven getal n.
| Definities Twee getallen a en b heten relatief priem ook wel onderling ondeelbaar, indien ggd(a, b) =1 Het aantal positieve getallen kleiner of gelijk aan n (ook positief) dat relatief priem is met n wordt aangegeven met f(n). f(n) heet de functie van Euler of ook wel indicator van Euler (Leonard Euler, 1707-1783, Zwitserland). |
Voorbeeld
f(1) =1, immers alleen (1,1)
= 1
f(2) = 1 = 2 -1, immers (1,1)
= 1
f(3) = 2 = 3 -1, immers
(1,3)1= 1, (2,3) = 1
f(4) = 2, omdat alleen (1,4)
= 1 en (3,4) = 1
f(5) = 4 = 5 - 1, omdat (1,5)
= 1, (2,5) = 1, (3,5) = 1, (4,5) = 1
f(6) = 2, omdat (1,6) = 1,
(5,6) = 1
f(7) = 6 = 7 -1 (!!)
....
[einde Voorbeeld]
| Stelling 15 ALS n = DAN f(n) = |
1e Bewijs:
Om f(n) te bepalen moeten
tellen hoeveel natuurlijke getallen kleiner of gelijk aan n met
n onderling ondeelbaar zijn.
Het aantal p1-vouden onder de getallen 1, 2, ..., n is gelijk
aan n/p1.
Het aantal niet deelbaar is door p1, is dus gelijk aan n - n/p1
= n/p1(p1 - 1).
Het aantal getallen uit 1, 2, ..., n dat niet deelbaar is door p1
en ook niet deelbaar is door p2 is dan gelijk aan
n/p1(p1 - 1) - n/(p1p2)(p1
- 1) = n/(p1p2)(p1 - 1)(p2 -
2)
Zetten we dit proces voort tot we ook pr hebben gehad, dan is
dus
f(n) = n/(p1p2...p r)
. (p1 - 1)(p2 - 1)...(pr - 1)
= n (1 - 1/p1)(1 - 1/p2)...(1 - 1/pr) �
Voorafgaande aan een tweede bewijs vermelden we, zonder bewijs, de
| Hulpstelling Voor de onderling ondeelbare getallen m en n geldt f(mn) = f(m) . f(n). |
2e Bewijs van Stelling 15:
Op basis van de hulpstelling kunnen we schrijven
![]()
We bekijken nu de factor met pi.
De getallen uit de verzameling 1, 2, ..., piai
die deelbaar zijn door pi zijn:
1pi, 2pi, 3pi, 4pi,
..., piai-1pi
Dus zijn er piai
- piai-1pi
die onderling ondeelbaar zijn met piai.
Dus f (piai
) = piai (1
- 1/pi)
De stelling volgt nu uit de bovenstaande schrijfwijze (gebaseerd op de hulpstelling) van f(n). �
Opmerkingen
[1]
In het voorbeeld hebben we reeds gezien, dat voor
een priemgetal p geldt
f(p) = p - 1
Deze eigenschap volgt het eenvoudigst uit de finitie van f
Volgens Stelling 15 is f(p)
= p(1 - 1/p) = p -1.
[2]
Voor toepassingen van de indicator van Euler, zie de paragraaf Gereduceerd restsysteem op de
pagina "Congruenties".
[einde Opmerkingen]
[deelbaar.htm] laatste wijziging op: 12-01-2018