| figuur 1 | 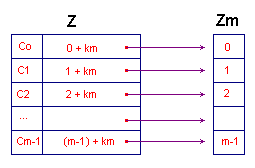 |
Overzicht ][ DK & Getallentheorie
| Definitie Als voor de gehele getallen a en b en een positief geheel getal m geldt m | (a-b) dan zeggen we dat a en b congruent modulo m zijn. Schrijfwijze: a ? b (mod m) of soms ook a = b (mod m). |
| Stelling 1 Voor congruenties (mod m) geldt
|
Bewijs:
De eigenschappen (i), (ii), (iii) volgen direct uit de definitie, immers a - a ? 0, a-b = -(b-a) en a-c = (a-b) +(b-c).
(iv)
Voor a, b en m geldt volgens de delingsalgoritme (op de pagina "Deelbaarheid"):
a = q1m + r1 met r1 < m
b = q2m + r2 met r2 < m
zodat
a - b = (q1-q2)m+ (r1-r2)
waarbij 0 ? (r1-r2) < m
Deze laatste ongelijkheid is te schrijven als 0 ? (r1-r2)
? m-1
Als nu ook moet gelden m | (a-b), dan is m | (r1-r2). En dan volgt
r1 = r2. ?
2. Congruentie- of restklassen
Door een congruentie (mod m) wordt de verzameling der gehele getallen opgedeeld in congruentieklassen
of restklassen die vastgelegd worden door Eigenschap IV van
Stelling 1.
Er zijn nu m congruentieklassen C0, C1, ,,,, Cm-1.
Een getal behoort tot Cr, dan en slechts dan als zijn hoofdrest bij deling door m
gelijk is aan r.
Elke klasse Cr (voor r = 0, 1, ..., m-1) in de verzameling Z van de gehele getallen bestaat daardoor uit de
getallen r + km (met k = 0, ?1, ?2, ...) (zie figuur 1).
| figuur 1 |  |
| Stelling 2 - Rekenregels Voor a ? b (mod m) en c ? d (mod m) geldt
|
Bewijs:
(i) a - b = pm, c - d = qm. Dus (a-b) + (c-d) = (p+q)m of (a+c) - (b+d) = rm, zodat a+c ? b+d (mod m).
(ii) ac - bd = ac - bc + bc - bd = (a-b)c + (c-d) b = pm . c + qm .
d = (pc+qd)m, zodat m | (ac - bd).
(iii) Zij d = ggd(m,n) en m = dm1, n = dn1 zodat dus ggd(m1,n1)=1
Als an ? bn (mod m), dan dm1 | (a-b)dn1
of m1 | (a-b)d, dus m1 | (a-b) waaruit a = b (mod m1 =
m/d ).
Voor het omgekeerde leiden we uit m1 | (a-b) af, dat dm1 | (a-b)d1.
Waaruit het gestelde volgt.?
Gevolg
Uit Stelling 2 (iii) volgt nu
| Stelling 2 (iv) Uit an ? bn (mod m) volgt dat a ? b (mod m) onder voorwaarde dat ggd(m,n) = 1. |
[einde Gevolg]
| Definitie De verzameling {x0, x1, ..., xm-1} heet een volledig restsysteem (mod m) als xi een element is van Ci (met i =0, 1, ..., m-1). |
Voorbeeld
{ 0, 1, 2, 3, 4, 5, 6 } is een volledige restsysteem (mod 7)
{ 0, 1, -1, 2, -2, 3, -3 } is eveneens een volledig restsysteem (mod 7)
[einde Voorbeeld]
| Stelling 3 [1] Is {x0, x1, ..., xm-1} een volledig restsysteem (mod m) dan is {ax0 +b, ax1 + b, ..., axm-1 + b} eveneens een volledig restsysteem (mod m) mits ggd(a,m) = 1 (b willekeurig). [2] Zijn {x1, ..., xm}(mod m) en {y1, ..., yn}(mod n) volledige restsystemen dan is { nxi + myj | i=1, .., m, j = 1, ..., n } een volledig restsysteem (mod mn) mits ggd(m,n) =1. |
Bewijs: (volgt) ?
3.2. Gereduceerd restsysteem, samenhang met de indicator van Euler
| Stelling 4 Heeft een restklasse (mod m) een element a, dat relatief priem is met m, dan is elk element van die restklasse relatief priem met m. |
Bewijs:
Als a ? b (mod m), dan is a-b = km (voor zekere k). Nu is dus
ook ggd(a, m) = ggd(b + km), m) en dus ook ggd(a, m) = ggd(b,m).
a en b behoren tot dezelfde restklasse, dus ook ggd (b,m) = 1. b is dus relatief priem met
m. ?
Gevolg
In de verzameling {0, 1, 2, ..., m1}, een volledig restsysteem module m, zijn er f(m) getallen die relatief priem zijn met m.
Hierbij is f(m) de zogenoemde indicator
van Euler.
Er zijn dus f(m) restklassen die bestaan uit getallen die met m
onderling ondeelbaar zijn.
[einde Gevolg]
We defini?ren op basis hiervan
| Definitie Een gereduceerd restsysteem (mod m) is een deelverzameling van een volledig restsysteem (mod m) bestaande uit f(m) restklassen, waarvan de elementen relatief prime zijn met m. |
Voorbeeld
{ 0, 1, 2, 3, 4, 5, 6 } is een volldige restsysteem (mod 7).
{ 1, 2, 3, 4, 5, 6 } is een gereduceerd restsysteem (mod 7). Merk op dat f(7) = 6, immers 7 is een priemgetal.
{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } is een volledig restsysteem (mod 10).
{ 1, 3, 7, 9 } is een gereduceerd restsysteem (mod 10). We weten, dat f(10)
= 4.
[einde Voorbeeld]
| Stelling 5 [1] Is { x1, x2, ..., xf(m) } een gereduceerd restsysteem (mod m), dan is { ax1, ax2, ..., axf(m) } een gereduceerd restsysteem (mod m), mits ggd(a,m) = 1. [2] Zijn { x1, x2, ..., xf(m) } (mod m) en { y1, y2, ..., yf(m) } (mod n) gereduceerd restsystemen, dan is ook { nx i + my j | ...} een gereduceerd restsysteem (mod mn), bestaande uit f(mn) = f(m) . f(n) elementen. |
Bewijs: (volgt).?
| Stelling 6a - Stelling van Euler ALS ggd(a, m) = 1 DAN af(m) ? 1 (mod m). |
Bewijs:
Zij n = f(m). En zij verder { x1, x2,
..., xn } een gereduceerd restsysteem (mod m).
Uit Stelling 5.1 volgt dan, dat ook { ax1, ax2,
..., axn } een gereduceerd restsysteem (mod m) is.
Voor alle xi en axj geldt xj ?
axi (mod m), voor zekere i en j.
Vermenigvuldiging geeft dan
ax1 . ax2 ... axn ? x1x2...xn (mod m)
Dus
anx1x2 ... xn
? x1x2 ... xn
(mod m).
Omdat ggd(x1, x2, ..., xn, m) = 1 vinden we volgens
het Gevolg van Stelling 2 (iii):
af(n) ?
1 (mod m). ?
| Stelling 6b - Kleine stelling van Fermat ALS p is priem en ggd(a, p) = 1 DAN ap-1 ? 1 (mod p) voor iedere gehele a. |
Bewijs:
Volgens Stelling 6a vinden we direct ap-1 ? 1 (mod p), immers f(p) = p-1. ?
Opmerkingen
[1]
De Kleine stelling van Fermat wordt oa. gebruikt bij het onderzoek naar
priemgetallen.
Zie Appendix B bij de pagina "Mersenne-priemgetallen" voor een ander bewijs van de Kleine
stelling van Fermat.
[2]
De Kleine stelling van Fermat wordt ook wel geformuleerd als
| Kleine stelling van Fermat ALS p is priem en ggd(a, p) = 1 DAN ap ? a (mod p) voor iedere gehele a. |
Bewijs:
Voor ggd(a,p) = 1 hebben we ap-1 ? 1 (mod p),
volgens Stelling 6b. Vermenigvuldiging met a geeft, volgens
het Gevolg van Stelling 2 (iii),
ap ? a (mod p).
Is ggd(a, p) ongelijk aan 1, dan is ggd(a,p) = p, zodat p | ap, en dus ook p |
(ap - a), waaruit volgens de definitie volgt
ap ? a (mod p). ?
[einde Opmerkingen en Gevolg]
| Definitie Als ggd(a,m) = 1dan heet het kleinste positieve gehele getal r met a r ? 1 (mod m) de orde van a (mod m). |
Opmerking
De Stelling van Euler toont aan, dat r bestaat en dat r ?
f(m).
Als ggd(a,m) groter dan 1 is, dan bestaat zo'n getal r niet.
Immers, ar ? 1 (mod m) houdt in, dat ar
= 1 + km (voor zekere k). Voor d = ggd(a,m) blijkt dan, als r > 0, dat d | 1.
Dus d = ggd(a,m) = 1.
[einde Opmerking]
Voorbeelden
[1] We kiezen m = 7. Dan is f(7) = 6.
Een gereduceerd restsysteem (mod 7) is dan { 1, 2, 3, 4, 5, 6 }.
In figuur 2 staan machten van a, waarbij a element is van bovenstaand gereduceerd rest
systeem.
| figuur 2 |  |
Tabel van an (mod 7) waarin {a} een gereduceerd restsysteem (mod 7) is |
We zien uit figuur 2, dat
| orde r gelijk aan | voor a gelijk aan |
| 1 | 1 |
| 2 | 6 |
| 3 | 2, 4 |
| 6 | 3, 5 |
Merk op, dat de delers van f(m) alle voorkomen als orde.
We zullen bewijzen (zie Stelling 8) dat voor de orde r
van een a (mod m) geldt, dat r | f(m).
Dat echter niet alle delers van f(m) als orde voorkomen blijk
in het tweede voorbeeld.
[2]
Kies m = 21. Dan is f(21) = 21 (1-1/3)(1-1/7)
= 2 . 6 = 12.
Een gereduceerd restsysteem (mod 21) is dan { 1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20 }.
In figuur 3 staan de machten van a.
| figuur 3 |  |
Tabel van an (mod 21) waarin {a} een gereduceerd restsysteem (mod 21) is |
Uit figuur 3 blijkt
| orde r gelijk aan | voor a gelijk aan |
| 1 | 1 |
| 2 | 8, 13, 20 |
| 3 | 4, 16 |
| 4 | geen |
| 6 | 2, 5, 10, 11, 17, 19 |
| 12 | geen |
N.B. We zien nu, dat niet alle delers van f(m)
als orde voorkomen.
[einde Voorbeelden]
Voor de orde van a hebben we de volgende eigenschappen
| Stelling 7 Als ggd(a,m) = 1 en als r de orde van a (mod m) is, dan [1] 1, a, a2, ..., ar-1 zijn incongruent (mod m) [2] Voor n > 0 is er een uniek getal s met 0 ? s < r zodat an ? as (mod m) [3] an ? 1 (mod m) DESDA r | n [4] ALS b ? a (mod m), DAN de orde van b (mod m) is gelijk aan de orde van a (mod m) |
Bewijs:
[1]
Bewijs uit het ongerijmde.
Stel er zijn u en v met au ? av (mod m)
waarbij 0 ? u < v < r.
Dan is 0 < v-u < r. Dus ook au ? au+(v-u)
(mod m).
Omdat ggd(au,m) = 1 hebben we (bij deling door au) av-u ? 1 (mod m).
Maar nu is v-u kleiner dan r, en dat is in tegenspraak met r is het kleinste getal
waarvoor ar ? 1 (mod m). ?
[2]
Volgens de delingsalgoritme zijn er getallen q en s met
n = qr + s waarbij 0 ? s < r
Nu is
an = aqr + s = (ar)q . as
? 1 . as = as (mod
m).?
[3]
Uit Stelling 5.2 volgt dat nu s = 0. Dus n = qr, waaruit r | n.?
[4]
Als b ? a (mod m) dan is ook bn ?
an (mod m) voor iedere positieve n.
Dus bn ? 1 (mod m) dan en slechts dan als an
? 1 (mod m).
Dit geldt dus ook voor r = n.?
| Stelling 8 ALS r is de orde van a (mod m), DAN r | f(m). |
Bewijs:
Volgens de Stelling van Euler is af(m)
? 1 (mod m). Uit Stelling 7.3 volgt dan
eenvoudig, dat r | f(m).?
Opmerking
Uit deze stellling kunnen we dus de resultaten in de beide voorbeelden
mbt. de deelbaarheid van de orde van a (mod m) op f(m)
verklaren.
[einde Opmerking]
[congruent.htm] laaste wijziging op: 05-10-2009 (18-09-1999)