FregierKegelsnede

Beschrijving
De macro tekent het Fr�gier-punt van een punt op een kegelsnede (H, E, P)

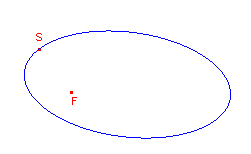De helptekst luidt:
"Constructie van het punt van Fr�gier van een punt S op een kegelsnede
- Selecteer het punt S (op de kegelsnede) en de kegelsnede"

[1]
Het Fr�gier-punt van een kegelsnede onstaat bij een involutie op die kegelsnede.
Zie verder de paragraaf Fr�gier-punt.
[2]
De macro:FregierKegelsnede wordt gebruikt bij de definitie van de macro:AssenKegelsnede (alleen ellips en hyperbool).

We construeren het Fr�gier-punt van een punt S via twee willekeurige punten A en B op de kegelsnede.
De involutie vastgelegd door de lijnen SA met de loodlijn in S daarop en de lijn SB met de loodlijn daarop, geeft bij snijding van de bijbehorende koorden, het Fr�gier-punt van S (zie figuur F2)

Fr�gier-punt
Een involutie van een kegelsnede is een afbeelding f van die kegelsnede op zichzelf waarbij voor elk punt X van die kegelsnede geldt
f(f(X)) = X

Stelling van Fr�gier
Zijn A, A', B, B' en P, P' zes punten van een kegelsnede en is f een involutie op die kegelsnede, met f(A)=A', f(B)=B', dan
f(P) = P' desda PP' gaat door het snijpunt van AA' en BB' (zie figuur F1).

In het bijzonder, bij ligging van een punt S op de kegelsnede, induceren de koordes die vanuit S onder een rechte hoek worden gezien een involutie op de kegelsnede. Deze koordes gaan dus alle door een vast punt.
Dit punt heet het Fr�gier-punt van S ten opzichte van de kegelsnede (zie figuur F2).

figuur F3		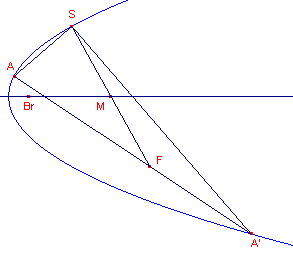Gevolgen [1] Het Fr�gier-punt van een punt op een cirkel is het middelpunt van die cirkel. [2] Als de kegelsnede een parabool is, dan ligt het midden van het lijnstuk SF op de as van de parabool (zie figuur F3).
figuur F4		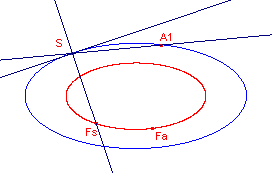[3] Zie figuur F4. We bekijken nu een vast punt S op een kegelsnede en een variabel punt A (in de figuur het punt A1). Het Fr�gier-punt van S is F_s; het Fr�gier-punt van A is F_a (zie figuur F4. Als nu A naar S nadert, dan nadert F_a naar F_s. De lijn SA nadert dan tot de raaklijn in S. We hebben hier dus een eenvoudige manier om de normaal in een punt van de kegelsnede te tekenen (en dus ook een raaklijn in een punt aan de kegelsnede)..

De verzameling van de punten F_a is een kegelsnede, die gelijkvormig is met de oorspronkelijke. Het gelijkvormigheidspunt is het middelpunt van de kegelsnede.
Verbinden we zo'n punt F met het middelpunt van de kegelsnede, dan krijgen we dus een middellijn van die kegelsnede.

figuur F1		figuur F2