 |
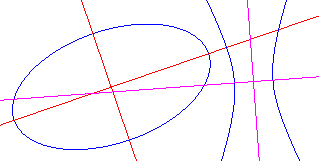
De helptekst luidt: "Constructie van de assen van een kegelsnede - Selecteer de kegelsnede" |
Beschrijving | Bijzonderheden | Constructie ][ Kegelsneden-macro's
Beschrijving
De macro tekent de beide assen van een kegelsnede
(ellips of hyperbool).
 |
De helptekst luidt: "Constructie van de assen van een kegelsnede - Selecteer de kegelsnede" |
| De as van een parabool kan niet geconstrueerd worden met deze
macro. Zie hiervoor de macro:AsParabool. |
Constructie
De constructie van de macro is gebaseerd op het feit, dat assen van een kegelsnede (E of
H) toegevoegde middellijnen zijn.
Daarnaast wordt gebruik gemaakt van het zogenoemde punt
van Fr�gier van een punt de kegelsnede.
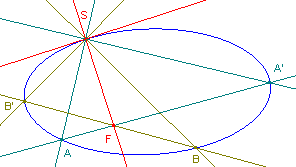 |
Elkaar in S (op de kegelsnede) snijdende loodlijnen bepalen een involutie
van de kegelsnede. In de figuur hiernaast zijn AA' en BB' paren van zo'n involutie. De lijnen AA' en BB' snijden elkaar in het punt van Fr�gier van het punt S. De lijn door F en S is de normaal van de raaklijn in S aan de kegelsnede. |
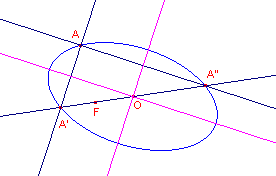 |
Ook toegevoegde middellijnen induceren een involutie op de kegelsnede. De assen zijn dan de loodrechte lijnen van die involutie. We bepalen dus eerst het Fr�gier-punt F van een willekeurig punt A van de kegelsnede en vervolgens het middelpunt O van de kegelsnede. De punten A' en A" zijn de snijpunten van OF en de kegelsnede. De lijnen door O evenwijdig met AA' en AA" zijn dan de assen van de kegelsnede. Voor de constructie van het Fr�gier-punt is gebruik gemaakt van de macro:FregierKegelsnede. Voor de constructie van het middelpunt is gebruik gemaakt van de macro:MiddelpuntKegelsnede. |