Overzicht ][ Alle werkbladen | Meetkunde | Cabri
Overzicht - Het punt van Fermat en de driehoek van Napoleon
Formulering van het
probleem
We gaan uit van een driehoek waaraan als enige
beperking wordt opgelegd, dat alle hoeken kleiner moeten zijn dan 120�.
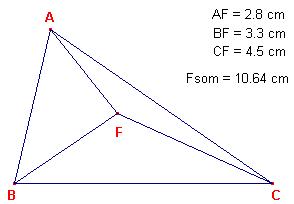
We zoeken binnen de driehoek een punt F waarvoor som van de afstanden tot de
hoekpunten zo klein mogelijk is (zie figuur 1).
| figuur 1 | |
 |
Ophalen van de figuur in Cabri Geometry |  |
Animatie met CabriJava | (*) |
| (*) | Voor het ophalen van de figuur in Cabri
Geometry is het noodzakelijk dat Cabri
II is ge�nstalleerd op het gebruikte computersysteem, waarbij de
Map-opties voor "Cabri-g�om�tre II Figure" en "Cabri-g�om�tre II
Macro" op de juiste wijze zijn ingesteld. Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren. Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download). |
Intermezzo 1
In hetgeen volgt zullen we een aantal malen op
een lijnstuk een gelijkzijdige driehoek moeten construeren.
Een macro hiervoor wordt hieronder beschreven.
| figuur 2a |  |
De macro:GelijkzDriehoek staat nu ook in het Macro-menu.
|
Ophalen van de figuur in Cabri Geometry | |
Animatie met CabriJava |
Verder zoeken
- het punt van Fermat
Het probleem bij het vinden van de minimale waarde van Fsom ligt
voor een deel in het feit, dat de drie lijnstukken eenzelfde eindpunt (namelijk het punt
F) hebben.
We construeren daarom een figuur waarin FA + FB + FC op en andere manier kan worden
bekeken.
| figuur 2b |  |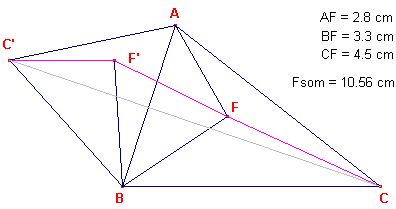
In figuur 2b is driehoek ABC’
een gelijkzijdige driehoek die "uitwendig" beschreven is op de zijde AB.
Driehoek BFF’ is eveneens gelijkzijdig en "naar buiten" beschreven op het
lijnstuk BF.
Kies nu weer het werkblad waarop een gedeelte van figuur 2 staat (je eerste werkblad; via het Venster-menu).
We noemen het punt binnen de driehoek waarvoor de som van
de afstanden tot de hoekpunten van de driehoek minimaal is, het punt van Fermat
van de driehoek (ook wel Fermat-punt; naar Pierre de Fermat, 1601-1665).
Het Fermat-punt van een driehoek wordt ook wel het punt van Torricelli (Evangelista Torricelli, 1608-1647) genoemd. Het
probleem is namelijk door Fermat ter oplossing aan Torricelli voorgelegd.
De oplossing van Torricelli is in 1659 gepubliceerd door Viviani, een
leerling van Toricelli.
|
Ophalen van de figuur in Cabri Geometry | |
Animatie met CabriJava |
We zullen nu proberen een constructie van de ligging van het punt F te vinden (en niet een benadering ervan, zoals hierboven).
| figuur 3 |  |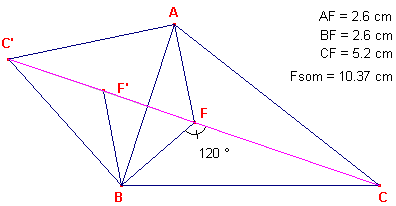
Ga ervan uit dat de punten F en F’ op het lijnstuk CC’ liggen (zie figuur 3)
|
Ophalen van de figuur in Cabri Geometry | |
Animatie met CabriJava |
Opdracht 3
Op basis van opdracht 2 kunnen we nu het
Fermat-punt van een driehoek ABC construeren.
Hieronder staan de constructiestappen.
|
Ophalen van de figuur in Cabri Geometry | |
Animatie met CabriJava |
Intermezzo 2
Voor het tekenen van de omgeschreven cirkel (omcirkel) van een
driehoek is het gebruik van een macro erg handig, temeer daar dat in hetgeen volgt nog een
enkele keer voorkomt.
Wellicht staat op de disk(ette) die je gebruikt, al een dergelijke macro. Mogelijke namen
zijn CIRCSCR.MAC, OMCIRKEL3P.MAC of CIRKEL3P.MAC (zie ook de pagina macro:Omcirkel3P)
Je kunt die macro opnemen in je huidige constructie via het Bestand-menu.
De macro staat daarna als laatste in het Macro-menu.
Opdracht 4
(facultatief)
Je kunt natuurlijk de macro ook zelf construeren.
| figuur 4 |  |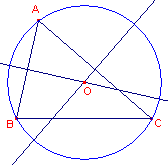
De macro:Omcirkel3P is nu te vinden in het Macro-menu van je huidige constructie.
Een
eigenschap van het Fermat-punt
Hierboven (in opdracht 3) is het Fermat-punt van
driehoek ABC gevonden met behulp van een gelijkzijdige driehoek op de zijde AB.
Natuurlijk had je daarvoor ook een gelijkzijdige driehoek op de zijde BC of op de zijde CA
kunnen kiezen (zie figuur 5).
| figuur 5 |  |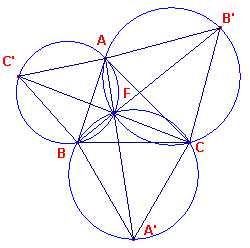
|
Ophalen van de figuur in Cabri Geometry | |
Animatie met CabriJava |
Merk op, dat nu hoek AFB = hoek BFC = CFA = 120�.
Het punt F heet vanwege deze eigenschap ook wel het isogonaal punt van de
driehoek: elke zijde wordt vanuit F onder dezelfde hoek (nl. 120�) gezien.
De
Napoleon-driehoek van een driehoek
We bekijken nu de driehoek met als hoekpunten de middelpunten van de
omcirkels van de buitenwaarts op de zijden van driehoek ABC beschreven gelijkzijdige
driehoeken (zie driehoek PQR in figuur 6).
| figuur 6 |  |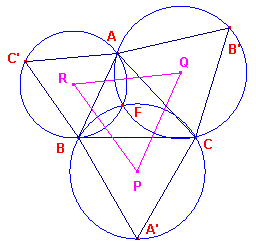
Deze driehoek heet de Napoleon-driehoek
van driehoek ABC.
De driehoek is inderdaad genoemd naar de Franse keizer Napoleon Bonaparte
(1768-1821). Verondersteld wordt dat deze in ieder geval enige belangstelling heeft gehad
voor de wiskunde.
|
Ophalen van de figuur in Cabri Geometry | |
Animatie met CabriJava |
Tenslotte:
rekenen aan Fsom
Natuurlijk is de waarde van Fsom afhankelijk van de lengtes van de
zijden van de driehoek.
Stel a, b, c zijn de lengtes van de zijden van de driehoek.
Verder is O de oppervlakte van driehoek ABC.
Download
De in het werkblad gebruikte Cabri-figuren kunnen via deze website in
��n bestand worden gedownload (de naamgeving van de figuren in dit bestand wijkt
af van de naamgeving in dit html-werkblad).
Naast de figuren zijn ook de gebruikte macro's in het bestand opgenomen, alsmede enkele
figuren waarin andere eigenschappen van het Fermat-punt en de Napoleon-driehoek worden
getoond.
Ook zijn figuren opgenomen met de stelling van Th�bault, de stelling
van Van Aubel (zie de betreffende webpagina)
en de stelling van Napoleon-Barlotti, die deels terug te voeren zijn op
constructies en eigenschappen die behandeld zijn in dit werkblad.
Klik hier om het downloaden van
het bestand te starten [34Kb, ZIP-formaat].
Het werkblad zelf is ook in PDF-formaat beschikbaar:
fermatnapo.pdf
[65Kb]
[fermatnapo.htm] laatste wijziging op: 13-02-2009 (27-12-2004)