Over vierhoeken
Overzicht ][ Meetkunde | Cabri
1. Definities ![]()
We geven hieronder enkele definities die betrekking hebben op vierhoeken;
daarbij gaan we uit van de "gebruikelijke" schoolwiskunde.
In een enkel geval worden twee definities (a en b) gegeven.
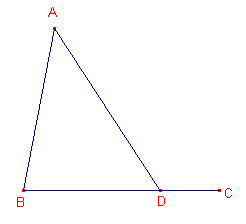
| Definitie 1a Een vierhoek is een figuur bestaande uit 4 punten en hun verbindingslijnstukken. |
| . |
 |
 |
| figuur 1 | figuur 2 |
Correct? Nee, immers in figuur 1 staat een driehoek(ige figuur).
Maar er is meer.
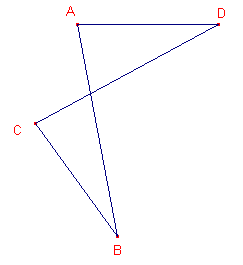
Ook de "vierhoek" in figuur 2 wordt meestal niet tot de vierhoeken gerekend
(hoewel daar niets tegen is).
| Definitie 1b: Vierhoek Een vierhoek is een figuur bestaande uit vier lijnstukken welke vier punten waarvan geen enkel drietal collineair is (op ��n lijn ligt) zo verbinden, dat 1) elk der vierpunten het eindpunt is van twee lijnstukken; 2) elk paar lijnstukken zonder gemeenschappelijk eindpunt geen snijpunt heeft. |
V e r d e r e n a a m g e v i n g
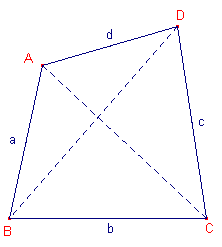 |
De vier lijnstukken heten de zijden van de vierhoek; hun
eindpunten noemen we de hoekpunten van de vierhoek. De door de zijden gevormde hoeken heten de hoeken van de vierhoek. Gebruikelijk is alleen vierhoeken te beschouwen waarvan de hoeken uitspringend (kleiner dan 180�) zijn. Dergelijke vierhoeken worden ook wel convexe vierhoeken genoemd (in tegenstelling tot concaaf). In de wiskunde op Nederlandse scholen worden de hoekpunten aangegeven met hoofdletters (meestal in tegenwijzerrichting); we spreken dus van vierhoek ABCD. De zijden AB, BC, CD, DA worden aangegeven met kleine letters (in die volgorde): a, b, c, d. De lijnstukken a en c en ook de lijnstukken b en d heten overstaande zijden. Twee zijden die een hoekpunt gemeenschappelijk hebben, heten opvolgende zijden. Die zijden heten de omliggende zijden van de hoek bij dat hoekpunt. De verbindingslijnstukken van de overstaande hoekpunten (A en C, B en D) heten diagonalen (AC en BD). |
| . |
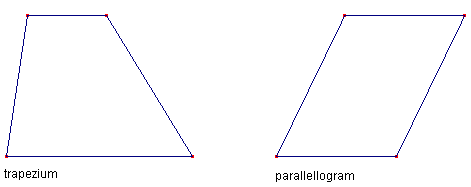
| Definitie 2a Een trapezium is een vierhoek waarvan precies ��n paar overstaande zijden evenwijdig is. |
| . |
| Definitie 2b: Trapezium Een trapezium is een vierhoek waarvan twee overstaande zijden evenwijdig zijn. |
Staat er in definitie 2b hetzelfde als in 2a?
Nee, in 2a wordt uitgesloten dat het "andere" paar overstaande zijden ook
evenwijdig is, maar (we spraken af) om een vierhoek trapezium te noemen, is het
voldoende dat er een (ten minste ��n) paar zijden evenwijdig is.
Opmerkingen
[1]
Het woord trapezium komt van het Grieks trapezion (uitspraak:
trap�dzion), dat een verkleinwoord is van het Grieks trapeza
(uitspraak: trap�dza), dat tafel betekent.
Bij Euclides (~300 vC) wordt het woord gebruikt voor een willekeurige
vierhoek (zie Definitie 1b). Heron onderscheidt (als eerste) trapezia (uitspraak: trap�dzia; onze trapezia) en trapezoeidh (trapezo�den = willekeurige vierhoeken).
[2]
Bijzondere trapezia zijn: gelijkbenig trapezium ("opstaande
zijden" zijn gelijk) en rechthoekig trapezium (een opstaande zijde
staat loodrecht op de evenwijdige zijden)
[einde Opmerkingen]
 |
| . |
| Definitie 3: Parallellogram Een parallellogram is een vierhoek waarvan de beide paren overstaande zijden evenwijdig zijn. |
Kiezen we 2b als definitie voor een trapezium, dan is een parallellogram dus ook een trapezium.
Opmerking
Het woord parallellogram komt van het Griekse (bijvoeglijk gebruikte) parallhlogrammon, bij het (meestal weggelaten) zelfstandig naamwoord schma (uitspraak: sch�ma), met de betekenis "door evenwijdige
lijnen begrensde figuur (parallhloV = parallel; grammh = lijn).
[einde Opmerking]
| Definitie 4a: Ruit Een ruit is een vierhoek waarvan alle zijden gelijk zijn. |
Opmerking
Natuurlijk is het mogelijk uit te gaan van een parallellogram:
| Definitie 4b Een ruit is een parallellogram waarvan twee opvolgende zijden gelijk zijn. |
Wellicht is dat, gezien de opbouw van de meetkunde (als deductieve wetenschap),
juister.
[einde Opmerking]
| Definitie 5a: Rechthoek Een rechthoek is een vierhoek waarvan alle hoeken gelijk (aan 90�) zijn. |
Opmerking
Ook hier zou het parallellogram als uitgangspunt kunnen dienen:
| Definitie 5b Een rechthoek is een parallellogram met een rechte hoek. |
Zie verder ook paragraaf 2.3, Een equivalentiebewijs.
[einde Opmerking]
| Definitie 6a: Vierkant Een vierkant is een vierhoek waarvan alle hoeken (90�) �n alle zijden gelijk zijn. |
Maar wellicht beter:
| Definitie 6b Een vierkant is een ruit met een rechte hoek. |
En dan vervolgens de vlieger. We geven de "eenvoudigste" definitie.
| Definitie 7: Vlieger Een vlieger is een vierhoek waarvan bij precies twee overstaande hoeken de omliggende zijden van die hoeken gelijk zijn. |
Opmerking
Vervangen we in de definitie "precies" door "ten minste", dan zijn de
ruit en het vierkant eveneens vliegers. Maar in de Nederlandse schoolwiskunde is dat niet
gebruikelijk. Gezien de mogelijke opbouw van de figuren, zou een en
andere echter aan te bevelen zijn.
[einde Opmerking]
2.
Opbouw en kenmerken ![]()
2.1. Opbouw
De opbouw van de verschillende verschillende figuren kunnen we als volgt schematiseren.
Uitgaande van een vierhoek kunnen we drie soorten "bewerkingen" uitvoeren:
1) we maken zijden evenwijdig;
2) we maken zijden aan elkaar gelijk;
3) we maken hoeken aan elkaar gelijk.
Een mogelijk 4e methode zou betrekking kunnen hebben op de diagnalen van de vierhoek
(gelijkheid, middendoor delen, loodrechte stand).
Zijden evenwijdig - Opvolgend onstaan dan: trapezium en
parallellogram.
Zijden gelijk - Enerzijds vlieger en dan ruit, anderzijds gelijkbenig
trapezium (en dan het parallellogram of wederom de ruit).
Hoeken gelijk - Enerzijds het gelijkbenig trapezium, gevolgd door de
rechthoek, anderzijds de vlieger, en daaruit weer het parallellogram en de rechthoek. Of
ook: rechthoekig trapezium gevolgd door rechthoek.
Combinaties van twee van de methodes leiden dan steeds tot het vierkant.
Klik hier ![]() voor een CabriJavapplet
waarin een en ander wordt zichtbaar gemaakt.
voor een CabriJavapplet
waarin een en ander wordt zichtbaar gemaakt.
2.2. Kenmerken en eigenschappen ![]()
We citeren de paragraaf Vierhoeken uit de Formulekaart Wiskunde havo/vwo
(Uitleg, Gele Katern nr. 12a, CEVO-98/257; zie de HTML-versie op de
website van de Nederlandse Vereniging van Wiskundeleraren) - met D is de hierboven staande
definitie aangegeven:
| De som van de hoeken van een vierhoek is 360� (hoekensom vierhoek). Equivalente definities en eigenschappen van een parallellogram: |
|
| a. | (D) Er zijn twee paren evenwijdige zijden. |
| b. | Er zijn twee paren gelijke overstaande zijden. |
| c. | Twee overstaande zijden zijn gelijk en evenwijdig. |
| d. | De diagonalen delen elkaar middendoor. |
| Equivalente definities en eigenschappen van een ruit: |
|
| a. | (D) Het is een parallellogram met vier gelijke zijden. |
| b. | Het is een parallellogram waarin een diagonaal een hoek middendoor deelt. |
| c. | Het is een parallellogram waarin de diagonalen elkaar loodrecht snijden. |
| Equivalente definities en eigenschappen van een rechthoek: |
|
| a. | (D) Het is een vierhoek met vier rechte hoeken. |
| b. | Het is een parallellogram met een rechte hoek. |
| c. | Het is een parallellogram met gelijke diagonalen. |
Opmerkelijk is, dat de vlieger en het vierkant in de Formulekaart niet worden genoemd.
2.3. Een equivalentiebewijs ![]()
De in paragraaf 2.2 (Kenmerken en eigenschappen) niet met (D)
aangegeven eigenschappen kunnen alle uit de definitie worden bewezen.
De equivalentie geeft aan, dat, als zo'n eigenschap als definitie gebruikt wordt, de in de
oorspronkelijke definitie genoemde eigenschap moet volgen uit de nieuwe definitie.
We geven een voorbeeld van een dergelijk bewijs (een equivalentiebewijs).
Gegeven: rechthoek ABCD, waarbij we als definitie gebruiken: Een
rechthoek is een parallellogram met een rechte hoek.
Te bewijzen:
a) ABCD heeft vier rechte hoeken;
c) ABCD heeft gelijke diagonalen.
Bewijs:
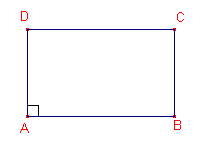 |
a. Zij hoek A recht. ABCD is een parallellogram: AB // CD (volgens de definitie van parallellogram). Zodat D = 90� (immers D + A = 180�; gevolg van F-hoeken). Evenzo: AD // BC. Zodat B = 90� (analoog). A + B + C + D = 360�, zodat ook C = 90�. |
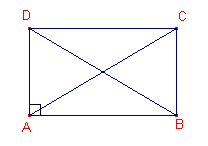 |
b. We dienen aan te tonen, dat AC = BD. We doen dit met congruentie: ABCD is een parallellogram. Volgens eigenschap b is dan: AD = BC AB = CD Uit a volgt: A = B De driehoeken ABD en BAC zijn congruent (ZHZ), waaruit volgt dat BD = AC |