Middelloodlijnen bij een vierhoek
Overzicht ][ Middelloodlijn | Meetkunde
1. Middelloodlijnen
![]()
Bij een willekeurige driehoek snijden de middelloodlijnen van de zijden elkaar in een punt
(zie de pagina "Middelloodlijn").
Dit is ook het geval bij een koordenvierhoek (zie de pagina "Koordenvierhoeken").
We onderzoeken hieronder de middelloodlijnen van de zijden van een vierhoek die geen omcirkel heeft.
| Stelling 2 De hoeken tussen de diagonalen in ABCD en in A'B'C'D' zijn gelijk. |
Bewijs:
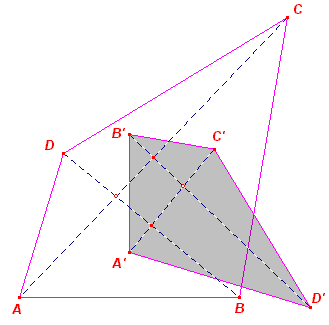 |
Voor het punt A' geldt: A'A = A'B en A'A = A'D. Zodat A'D = A'B A' ligt dus op de middelloodlijn van BD ......(1) Voor het punt C' geldt: C'B = C'C en C'C = C'D. Zodat C'B = C'D. C' ligt dus eveneens op de middelloodlijn van BD ......(2) Uit (1) en (2) volgt: A'C' is de middelloodlijn van DB. Zo is B'D' de middelloodlijn van AC. De hoek tusssen AC en BD is dus gelijk aan de hoek tussen A'C' en B'D'. � |
2. Een serie vierhoeken
![]()
We kunnen ook de middelloodlijnen tekenen van de zijden van A'B'C'D'.
Dit levert:
| Stelling 3 Bij een niet-koordenvierhoek A0B0C0D0 vormen we de vierhoek A1B1C1D1 bepaald door de middelloodlijnen van de zijden. Van deze laatste vierhoek doen we dat opnieuw, enzovoorts. In de rij van vierhoeken AiBiCiDi zijn de vierhoeken met i = 0, 2, 4, ... gelijkvormig; die met i = 1, 3, 5, ... eveneens. |
Bewijs:
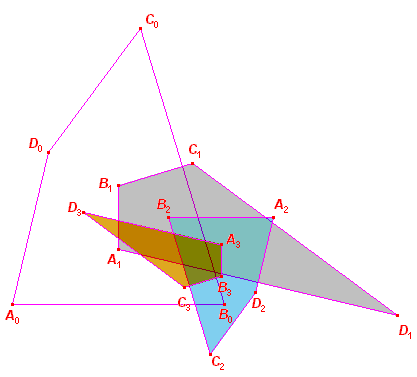 |
Voor A1B1B1D1 en A2B2B2D2
geldt uiteraard ook Stelling 1. De hoeken van de vierhoeken A0B0C0D0 en A2B2C2D2 zijn dus gelijk. Uit de constructie volgt voorts dat de overeenkomstige zijden van die vierhoeken evenwijdig zijn, immers B1 en D1 zijn middelpunten van de omcirkels van A0B0C0 en C0D0A0, waardoor B1D1 middelloodlijn is van A0C0. Evenzo is (bijvoorbeeld) A2C2 middelloodlijn van B1D1, zodat A2C2 // A0C0. Waardoor ook de diagonalen van A0B0C0D0 en A2B2C2D2 evenwijdig zijn. Deze vierhoeken zijn dus gelijkvormig (gelijkstandig, homothetisch). Enzovoorts... (Met dank aan Darij Grinberg.) � |