CabriFAQ 29

Cabri-FAQ (29)

Vorige

Begin

Volgende

Vraag 29
Hoe kun je een co�rdinatenstelsel op een lijn aanbrengen?

Antwoord
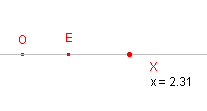
Onder een co�rdinatenstelsel op een lijn verstaan we een systeem waarmee de afstand van een willekeurig punt X op die lijn wordt vastgelegd als de verhouding van de afstand van dat punt tot twee vaste punten O (de oorsprong) en E (de eenheid) van die lijn (zie figuur 1). Als X en E een verschillende kanten van O liggen, dan dient de verhouding van een minteken te worden voorzien.

figuur 1a	figuur 1b
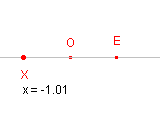		In figuur 1a is zo'n co�rdinatenstelsel aangebracht. De co�rdinaat van het punt X is hier 2,31. Hetgeen betekent, dat geldt: OX = 2,31 . OE. In figuur 1b heeft het punt X een negatieve co�rdinaat in het stelsel.

Methode 1
Het aanbrengen van een dergelijk systeem kan eenvoudig worden gerealiseerd door het "ingebouwde" assenstel van Cabri te gebruiken.

figuur 2

Constructiestappen bij de hiernaast staande figuur:
1, 2 - Punt(en) = O, E
3 - Lijn(O, E)
4 - NieuwAssenstelsel(O, E [dit punt]), willekeurige punt voor de y-as = E₂)
De stand van de y-as is voor ons doel niet van belang.
5 - PuntOpObject(3) = X, dus op de lijn door O en E; niet op de x-as.
6 - Co�rdinaten(X, x-as [dit co�rdinatensysteem])
Willen we alleen de x-co�rdinaat zien, dan moeten we deze overbrengen in een commentaarbox.
7 - Commentaar(type 'x =' en wijs de x-coordinaat van het punt X aan [Voeg dit getal toe])
Daarna kunnen we de beide co�rdinaten van het punt X, het assenstelsel en het punt E₂, indien gewenst, verbergen.

Klik hier voor een CabriJavapplet gebaseerd op Methode 1.

Methode 2
Bij deze methode gebruiken we geen xy-assenstel, maar een Cabri-functie, nl. SIGN. Deze functie heeft de volgende betekenis:
   SIGN( x ) = 1, als x > 0
   SIGN( x ) = 0, als x = 0
   SIGN( x ) = -1, als x < 0.
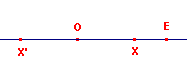
Om te bepalen of het punt X aan dezelfde kant van O ligt als het punt E, of aan verschillende kanten, gebruiken we het spiegelbeeld X' van X in het punt O (zie figuur 3a en 3b).

figuur 3a	figuur 3b
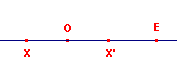		Merk op, dat in figuur 3a geldt: X'E > XE, en dus X'E - XE > 0 In figuur 3b geldt: X'E < XE, dus: X'E - XE < 0. Als X met O samenvalt is X'E - XE = 0. Op de waarde van X'E - XE kunnen we nu sign-functie toepassen, en zo de ligging van het punt X tov. het punt O vaststellen.

We geven hieronder de constructiestappen voor de macro:LijnCoordinaat.

figuur 4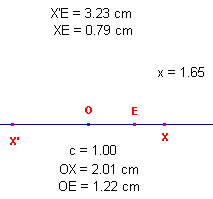

We gaan uit van de "in ligging" gegeven punten O, E en X (X is gekozen als object op de lijn OE).
1 - Afstand(X', E) = X'E (= a)
2 - Afstand(X, E) = XE (= b)
3 - Rekenmachine(type 'sign(', a, b, type ')', = ); en plaats het resultaat (= c) op het Cabri-scherm.
We moeten nu de lengte van OX normaliseren met de lengte van OE.
4 - Afstand(O, X) = a
5 - Afstand(O,E) = b
En vervolgens berekenen we de co�rdinaat van X met behulp van de waarde c (zie stap 3).
6 - Rekenmachine(a, /, b, *, c, =); en plaats het resultaat (= x) op het scherm.

We kunnen nu de macro:LijnCoordinaat vastleggen:
Beginobjecten: X, O, E (in deze volgorde)
Eindobjecten: het getal x; zie punt 6 (dus niet de tekst selecteren).

Klik hier voor een CabriJavapplet gebaseerd op Methode 2.

Opmerking
Zo op het oog geven beide methoden hetzelfde resultaat.
Echter, indien bij Methode 1 de positie van de punten O en E wordt gewijzigd, dan verandert de co�rdinaat van het punt X niet (zie de applet bij Methode 1). Het punt O is hier namelijk als 'startpunt' van de lijn gekozen.
Worden de punten O en E ook als object op een bestaande lijn gekozen, dan wijzigt de co�rdinaat van het punt X wel.
Krijgen bij Methode 2 de punten O en E een andere positie op de lijn (hoe ook aanvankelijk vastgelegd), dan wijzigt de co�rdinaat van het punt X altijd (zie de applet bij Methode 2).
[einde Opmerking]

Zie Download
Extra bestanden: LijnCoord(constr).fig, LijnCoordinaat.mac

Vorige

Begin

Volgende

[faq26.htm] laatste wijziging op: 28-08-02