1.1. Gegevens invoeren
We hebben een aantal eindcijfers van 40 leerlingen bij een examen wiskunde verzameld:
1. Gegevens
invoeren en statistische grootheden ![]()
1.1. Gegevens invoeren
We hebben een aantal eindcijfers van 40 leerlingen bij een examen wiskunde verzameld:
| cijfer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| frequentie | 0 | 1 | 1 | 3 | 9 | 13 | 6 | 4 | 2 | 1 |
Om deze gegevens te verwerken met de GR slaan we ze op in Lijsten (zie ook het werkblad
"Lijsten").
We gebruiken de lijsten L1 en L2. In L1 plaatsen we de
cijfers; in L2 zetten we de frequenties.
De [STAT] knop geeft toegang tot de statistische mogelijkheden van de TI83.
| 1. | Druk op [STAT]<Edit>1:Edit. Je krijgt nu een scherm met Lijsten. Maak deze lijsten zo nodig leeg met [MEM]4:ClrAllLists (sluit daarbij af met [ENTER]). Voer vervolgens de gegevens uit bovenstaande tabel in. Aan het eind van de lijst moet je dan iets hebben als hiernaast staat. |
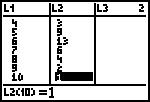 |
| . |
| Opmerking Om na te gaan, dat je inderdaad 40 cijfers hebt ingevoerd, kan je de waarden die in L2 staan, optellen. Ga met [Quit] naar het rekenscherm en kies [LIST]<Math>5:sum(. Voer nu L2 in (met [2nd][2]) en sluit af met [ ) ]. [einde Opmerking] |
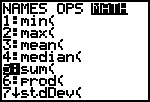 |
 |
We kunnen nu enkele statistische grootheden voor de eindcijfers berekenen.
We hebben hier als meetwaarden de getallen 1, 2, …, 10 (deze getallen staan in L1).
Willen we van die meetwaarden het gemiddelde uitrekenen (we krijgen daarnaast ook nog wat
andere waarden), dan gebruiken we de opdracht 1-Var
(we hebben slechts 1 variabele gemeten, namelijk het eindcijfer).
| . |
| 1.2. Statische grootheden Verklaring van de gegevens uit opdracht 3: |
|
| het gemiddelde van de cijfers | |
| S x = 242 | de som van alle cijfers |
| S x2=1566 | de som van de kwadraten van de cijfers |
| Sx=1.61… | de standaarddeviatie bij deling door 39 (deze waarde gebruiken we bijna nooit) |
| s x=1.59… | de standaarddeviatie bij deling door 40 |
| n=40 | het aantal cijfers (ook wel het aantal waarnemingen) |
| minX=2 | de kleinste waarneming |
| Q1=5 | het eerste kwartiel |
| Med=6 | de mediaan |
| Q3=7 | het derde kwartiel |
| maxX=10 | de grootste waarneming |
Opmerking
| 4. | Kies nu [STAT PLOT]. In dit scherm kan je drie verschillende "plots" vastleggen (>>>). | 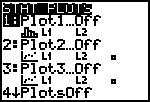 |
| 5. | Kies de eerste met 1:Plot1; deze plot staat in eerste instantie Uit
(Off). Zet op het volgende scherm Aan (On) met [ENTER]. |
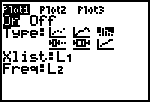 |
| Ook het derde icoon, achter Type, is hier geselecteerd.
Dit betekent dat er een histogram wordt getekend. Is dat niet het geval, plaats dan de cursor op dat icoon en bevestig je keuze opnieuw met [ENTER]. Vul vervolgens bij Xlist en Freq de namen van de lijsten (L1, weer met [2nd][1], en L2, weer met [2nd][2]) in. |
||
| 6. | Druk nu op [GRAPH]. Je krijgt nu in ieder geval een histogram te zien. Maar vermoedelijk staat dat niet erg fraai in beeld. Iets als (>>>): |
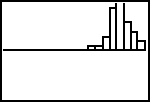 |
| In eerste instantie kan dat verbeterd worden met [ZOOM]9:ZoomFit (zie
>>>). Maar je verwacht toch op z’n minst 9 staven! De oorzaak hiervan is gelegen in het feit dat de TI83 wat anders omgaat met de gegevens dan je verwacht. |
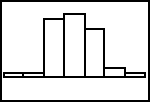 |
|
| 7. | Handiger is het om via [WINDOW] direct de (grens)waarden op de x-as
(horizontale as) in te stellen. Kies daarbij Xmin=1.5 (Xmin = minX – 0.5) en Xmax = 10.5 (Xmax = maxX + 0.5) De waarden minX en maxX heb je in paragraaf 1.2 gevonden met de opdracht 1-Var. Kies verder Xscl = 1. Je krijgt dan (>>>): |
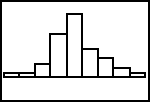 |
| 8. | Met de opdracht [TRACE] kan je over de toppen van de staven van het histogram "springen". Onder in het scherm staan dan de klassengrenzen (min en max) en de klassenfrequentie (n). |
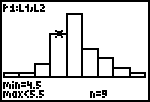 |
| 9. | Kies [STAT PLOT] 1:Plot1 | 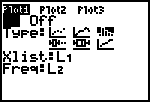 |
| Zet nu de cursor op het tweede icoon in de tweede
rij (achter Type). Selecteer deze optie (Boxplot). |
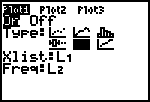 |
|
| 10. | Druk dan op [GRAPH]. | 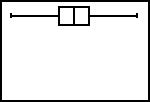 |
| 11. | Ook hier kan je met [TRACE]
de verschillende statistische grootheden bekijken. Eerst zie je de mediaan (Med). |
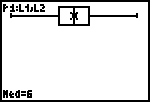 |
| Met [� ] en [� ] kan je vervolgens Q1, minX en Q3, maxX in beeld brengen. | 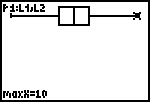 |
3. Download
![]()
Deze pagina is, niet meer beschikbaar in PDF-formaat.
[besstat.htm] laatste wijziging op: 19-01-18