Een eigenschap van het
hoogtepunt
Stelling | 1e
bewijs | 2e bewijs ][ Lijn van Steiner | DK
& Meetkunde
Stelling
In een driehoek liggen het hoogtepunt en het snijpunt van de hoogtelijn met de
omcirkel symmetrisch ten opzichte van de zijde waarop die hoogtelijn staat;
of
Het spiegelbeeld van het hoogtepunt van een driehoek in een zijde ligt op de omcirkel. |
We geven twee bewijzen van deze stelling geven (zie 1e bewijs en 2e bewijs)
1e Bewijs :
We willen aantonen (zie figuur 1), dat het punt Ha symmetrisch ligt met het
punt H ten opzichte van de lijn BC.
| figuur 1 |
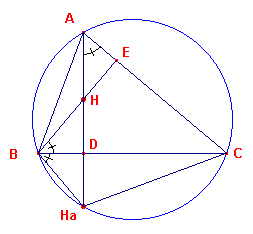 |
In de driehoeken AEH en BDH is ?E = ?D en ?H = ?H;
dus
?EAH = ?DBH.Verder
is ?HaAC = ?HaBC
(staan op gelijke bogen).
Uit beide volgt nu
?HaBD = ?HBD
Terwijl BD ^ HaH.
Hieruit volgt dan inmiddellijk, dat HD = HaD, zodat H en Ha
symmetrisch liggen ten opzichte van de zijde BC van de driehoek. ? |
Opmerking
Deze eigenschap wordt ook gebruikt bij het onderzoek naar de zogenoemde cirkel van Feuerbach (ook wel negenpuntscirkel
genoemd).
[einde Opmerking]
Klik hier om terug te gaan naar de tekst
op de pagina Steiner-lijn.
2e Bewijs
Dit bewijs maakt gebruik van de eigenschappen van een koordenvierhoek (zie figuur 2).
We tonen aan, dat het spiegelbeeld Ha van H in de zijde BC op de omgeschreven
cirkel van ABC ligt.
| figuur 2 |
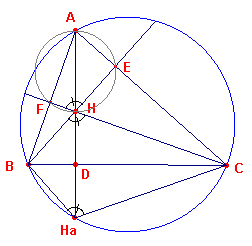 |
Uit de spiegeling in BC blijkt:
?BHC = ?BHaC.Verder
is in vierhoek AFHE ?E = ?F =
90?, zodat daarin ?H + ?A =
180?.
Maar dan geldt
?BAC + ?BHaC
= 180?
zodat ook ABHaC een koordenvierkoek (in de omgeschreven cirkel van ABC) is.
Dus Ha ligt op de omgeschreven cirkel van driehoek ABC. ? |
Klik hier om terug te gaan naar de tekst
op de pagina Steiner-lijn.

[steiner2.htm] laatste wijziging op: 23-12-2003

