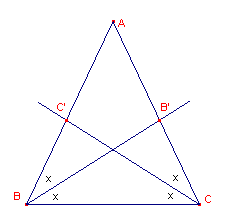
Nu geldt: BCC' @ CBB' (HZH), immers �B = �C, �C1 = �B1 (halve hoeken), BC = CB.
Waaruit volgt:
CC' = BB'. �
Inleiding | Bewijzen | Referenties ][ Meetkunde
1. Inleiding en probleemstelling
| Stelling 1 Elke gelijkbenige driehoek heeft twee gelijke bissectrices. |
Bewijs: zie figuur 1.
| figuur 1 |  |
In driehoek ABC zijn de B en C gelijke basishoeken. BB' en CC' zijn de
bissectrices daarvan. Nu geldt: BCC' @ CBB' (HZH), immers �B = �C, �C1 = �B1 (halve hoeken), BC = CB. Waaruit volgt: CC' = BB'. � |
We formuleren nu de omgekeerde stelling van stelling 1.
| Stelling 2 (Steiner-Lehmus) Elke driehoek met twee gelijke bissectrices is gelijkbenig. |
Kijken we naar dezelfde driehoeken (in figuur 2), dan kunnen we uit de gegevens niet besluiten tot congruentie.
| figuur 2 | 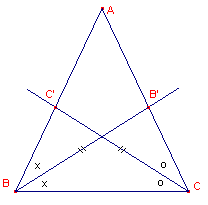 |
We zullen dus moeten besluiten tot een andere aanpak. Zie daarvoor paragraaf 2, Bewijzen. |
Stelling 2 is in 1840 als probleem door Lehmus (Daniel Christian
Ludolf Lehmus, 1780-1863, Duitsland), mogelijk door tussenkomst van C. Sturm,
voorgelegd aan Jakob Steiner (1796-1863, Zwitserland). Deze laatste
publiceerde een bewijs in het tijdschrift (Journal f�r die reine und angewandte
Mathematik, opgericht in 1826) van Crelle (August Leopold Crelle, 1780-1855, Duitsland).
Ook Lehmus zelf heeft een indirect bewijs gepubliceerd (Journal, 1850).
Een bewijs dat lijkt op dat van Lehmus, staat in paragraaf 2.
2. Bewijzen
Hieronder zijn enkele bewijzen van de Stelling van Steiner-Lehmus
vemeld.
De bewijzen zijn min of meer gerangschikt op jaar van eerste publicatie.
| 2.1. | 1820 | / D.Ch.L. Lehmus | |
| 2.2. | 1842 | / F.G. Hesse | |
| 2.3. | 1842 | / P. Rougevin | |
| 2.4. | 1880 | / F. Descubes | |
| 2.5. | 1906 | / M. Simon | |
| 2.6. | ?? | / Toepassing van de Stelling van Stewart | |
| 2.7 | 1961 | / H.G. Forder |
2.1. - D.Ch.L. Lehmus (1850, vermeld in [5])
| figuur 3 | 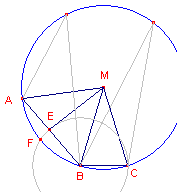 |
Indirect (zie nevenstaande figuren).
Bewijs: |
|
| figuur 4 | 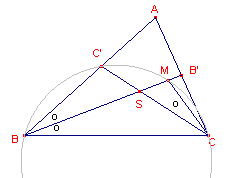 |
Bewijs: |
�CBC' < �MCB
< 90�
Volgens hulpstelling 1 is is dan CC' < BM, waaruit
BB' > BM > CC.'
Dus, kortgezegd:
Gevolg van Hulpsteling 2: Geen gelijke hoeken, dan geen gelijke
bissectrices.
De logische omkering van dit gevolg levert dan Stelling 2:
Gelijke bissectrices, dan gelijke hoeken. �
2.2. - F.G. Hesse (1842, vermeld in [2])
| figuur 5 | 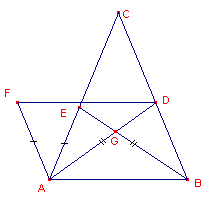 |
Direct bewijs (zie nevenstaande figuur). Construeer driehoek ADF zodat DF=AB en AF=AE. Nu is ADF @ EBA (ZZZ), waaruit volgt, dat �FAD = �AEB, en �ADF = �B. In de driehoeken AGE en BGD hebben we nu: �AEB + �A = �ADB + �B (beide zijn supplement van hoek G), zodat �FAD + �A = �ADB + �ADF, en dus �FAB = �BDF |
Dit laatste, samen met BA = FD en BF = FB, geeft
BAF @ FDB, waaruit we mogen afeiden AF = DB.
Dus AE = BD!
Uit de congruentie van de driehoeken ABE en BAD (ZZZ) volgt dan Stelling 2.
�
2.3. - P. Rougevin (1842, vermeld in [2])
| figuur 6 | 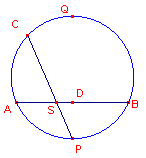 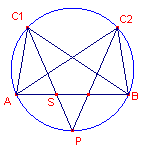 |
(In)direct bewijs (zie nevenstaande figuren).
Bewijs: |
|
| figuur 7 | 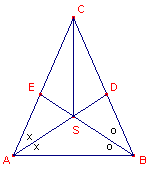 |
In driehoek ABC is AD = BE, met snijpunt S. CS is dus ook bissectrice van driehoek ABC. De driehoeken ADC en BEC voldoen nu aan de eisen van het Gevolg van Hulpstelling 3. Dus geldt: ADC @ BEC �f ADC @ EBC. Dit laatste geval is onmogelijk, want dan zou �ADC gelijk zijn aan �EBC, een buitenhoek van BDS. Dus volgt nu �CAD = �CBE, en dus �A = �B. � |
2.4. - F. Descubes (1880, vermeld in [1] en [2])
| figuur 8 | 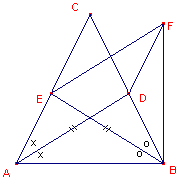 |
Indirect bewijs (zie nevenstaande figuur) Zij F het hoekpunt van het parallellogram ADFE. Nu is EF = AD = BE. Dus �EBF = �EFB. Stel nu dat A > B. Dus ook �A > �B, zodat �EFD > �EBD. Dus ook �DFB < �DBF |
Dus in driehoek BDF: DB < DF, of ook DB < AE.
Via de driehoeken ABD en BAE vinden we dan A < B.
Dit is in strijd met de verondersteling dat A > B.
Ook A < B leidt tot een contradictie.
Dus geldt A = B. �
2.5. - M. Simon (1906, vermeld in [1] en [2])
| figuur 9 |  |
Indirect bewijs (zie figuur 9) V(AB'B) = �BB' . c . sin�B V(CB'B) = �BB' . a . sin�B Voor de oppervlakte V van driehoek ABC hebben we dus: 2V = BB'(a+c)sin�B en dus ook 2V = CC'(a+b)sin�C, zodat (a+c)sin�B = (a+b)sin�C, waaruit volgt: c . sin�B - b . sin�C = a(sin�C - sin�B) ......(2.5.1) Stel nu B > C. |
Dan is cos�B < cos�C ......(2.5.2)
Uit de sinusregel volgt c . sinB =
b . sinC, met 2csin�Bcos�B = 2bsin�Ccos�C, zodat samen met
(2.5.2)
c . sin�B - b . sin�C > 0
Het linkerlid van (2.5.1) is dus positief; het rechterlid is echter negatief. Tegenspraak!
Ook B < C leidt tot een tegenspraak.
Zodat B = C. �
2.6. - Toepassing van de Stelling van Stewart (vermeld in [1] en [2])
Direct bewijs; zie figuur 9.
Volgens de bissectriceformule (een gevolg van de Stelling van Stewart) hebben we:
BB'2 = AB . CB - AB' . CB'
......(2.6.1)
Verder is volgens de bissectrice stelling AB' : CB' = AB : CB,
zodat voor zekere k geldt: AB' = kc en CB' = ka.
Voor k vinden we dan k = b/(a + c).
(2.6.1) geeft dan BB'2 = ac (1 - b2 / (a + c)2)
Evenzo: CC'2 = ab (1 - c2 / (a + b)2)
Gelijkstelling en uitwerking van de factoren levert:
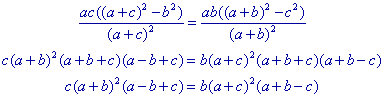
Verdere uitwerking geeft dan tenslotte:
(b - c)( a3 + 3abc + bc(b
+ c) + a2(b + c) )= 0
De tweede factor bestaat uit louter positieve termen. Dus moet gelden b - c = 0.
Zodat b = c. �
2.7. - H.G. Forder (1961, vermeld in [4])
| figuur 10 | 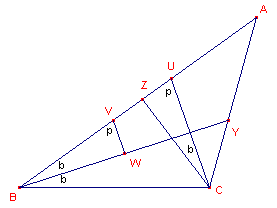 |
Indirect bewijs (zie nevenstaande figuur). Zij B de kleinste van de hoeken B en C van driehoek ABC. BY en CZ zijn de bissectrices van deze hoeken. Kies U op AZ zo, dat �ZCU = �B. Omdat driehoek UBC in B een kleinere hoek heeft dan in C, geldt BU>CU. Kies V op BU, zodat BV = CU. Kies W op BY zodat �BVW=�CUZ. De driehoeken BVW en CUZ zijn nu congruent (HZH), waaruit volgt dat BW = CZ. Nu is BY > BW (W en Y aan verschillende kanten van CZ), zodat BY > CZ. Enzovoorts. � |
| [1] | O. BOTTEMA: Hoofdstukken uit de Elementaire Meetkunde, Epsilon Uitgaven, Utrecht, 1997 | |
| [2] | O. BOTTEMA: Verscheidenheden, Ned. Verg. van Wiskundeleraren (Wolters-Noordhoff), 1977 | |
| [3] | J.A. MCBRIDE, Edinburgh Mathematical Notes, vol. 33 (1943), pag. 1-13 | |
| [4] | H.S.M. COXETER, Introduction to geometry, John Wiley & Sons, New York, 1961 | |
| [5] | H.S.M. COXETER, S.L. GREITZER: Geometry Revisited, Random House, New York, 1967 |
[steileh.htm] laatste wijziging op: 19-10-03