Propositie III-22
[ Elementen | DK & Meetkunde ]
Propositie III-22
Van vierhoeken in cirkels zijn de overstaande hoeken gelijk aan twee rechte [hoeken]. |
Is ABCD een cirkel, en is ABCD een vierhoek daarin (zie figuur 1).
Ik zeg nu dat de overstaande hoeken gelijk zijn aan twee rechte hjoeken.
| figuur 1 |
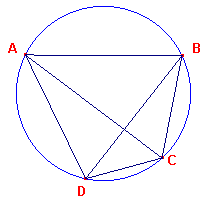 |
Zijn AC, BD verbonden.
Dan zijn, omdat in een willekeurige driehoek de drie hoeken gelijk zijn aan twee rechte
hoeken, de drie hoeken CAB, ABC, BCA van de driehoek ABC gelijk aan twee rechte hoeken.
Maar de hoek CAB is gelijk aan de hoek BDC, omdat ze op hetzelfde segment BADC staan
(beide staan op bg DC; DK);
en de hoek ACB is gelijk aan de hoek ADB, omdat ze op hetzelfde segment ADBC staan;
daarom is de gehele hoek ADC gelijk aan de hoeken BAC, ACB.
Hoek ABC wordt bij elk opgeteld; daarom zijn de hoeken ABC, BAC, ACB gelijk aan de hoeken
ABC, ADC. |
Maar de hoeken ABC, BAC, ACB zijn gelijk aan twee rechte hoeken;
daarom zijn de hoeken ABC, ADC ook gelijk aan twee rechte hoeken.
Op dezelfde manier kunnen we bewijzen, dat de hoeken BAD, DCB gelijk zijn aan twee
rechte hoeken.
Hetgeen te bewijzen was. ?
Klik hier  voor een animatie
van bovenstaande stelling.
voor een animatie
van bovenstaande stelling.

[propIII22.htm] laatste wijziging op: 25-02-2003
