Cel van Peaucellier
Inleiding | Bewijs | Rechtlijnige
beweging | Referenties ][ Inversie | DK & Meetkunde
1. Inleiding 
Een nog op te lossen probleem aan het einde van de 19e eeuw was een mechanisme waarmee de
inverse van een gegeven figuur kon worden getekend.
In 1864 slaagde een Franse legerofficier, A. Peaucellier (1832-1913),
erin een dergelijk apparaat te ontwikkelen.
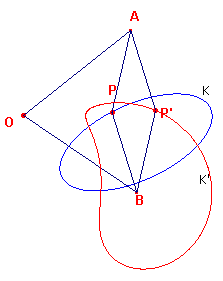
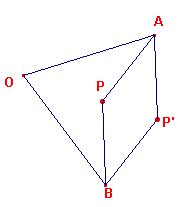
Het bestaat uit 4 gelijke stangen die een ruit (rhombus) APBP' vormen en 2 gelijke
(langere) stangen die verbonden zijn aan de beide overstaande hoekpunten A en B en aan een
vast draaipunt O (zie figuur 1).
| figuur 1 |
 |
Als een tekenpen wordt geplaatst in het punt P' en het punt P een kromme
lijn K volgt, dan tekent de pen de inverse van K. Bijzonder in dit geval is, dat indien
een 7e stang wordt gebruikt om het punt P op een cirkel door het punt O te houden, de
meetkundige plaats van P' een rechte lijn is.
Hiermee is het belangrijke mechanische probleem opgelost om een cirkelbeweging om te
zetten in een rechtlijnige beweging.
Een dergelijk mechanisme wordt onder meer gebruikt in (mechanische) naaimachines. |
2. Bewijs 
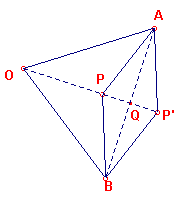
Zie figuur 3. Hierin is Q het centrum van de ruit.APBP'.
| figuur 3 |
 |
Nu is
| OP x OP' |
= |
(OQ - PQ)(OQ + PQ) = OQ2 - PQ2 |
|
= |
OQ2 + AQ2 - (AQ2 + PQ2) |
|
= |
OA2 - PA2 |
En deze laatste uitdrukking is constant.
P en P' zijn dus elkaars inverse. � |
3. Rechtlijnige beweging

Zoals reeds in de Inleiding is opgemerkt, kan via een 7e stang bereikt
worden, dat het punt P een cirkel beschrijft die door het punt O gaat.
Zie hiervoor figuur 4.
| figuur 4 |
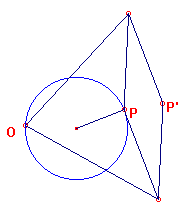 |
Als P de cirkel doorloopt, beschrijft het punt P' een rechte lijn. Een en
ander geheel volgens de theorie der inversie (Cirkels door
het punt O). Hiermee wordt dus een cirkelbeweging omgezet in een rechtlijnige.
Klik hier  voor een CabriJavapplet
van een dergelijke beweging. voor een CabriJavapplet
van een dergelijke beweging. |
4. Referenties 
[1] Howard Eves, A Survey of Geometry, Allyn and Bacon,
Inc., Boston - ISBN: 0-205-03226-5
In dit boek treffen we op de bladzijden 135-137 een kort historisch overzicht aan van de
uitvinding van de Peaucellier-cel.
[2] Leo's Lego
Designs - UvA, Amsterdam
[3] Analog device
for converting circular motion into linear - Cut-The-Knot, US
[4] Peaucellier
Inversor - CRC Encyclopedia, US
[5] Peaucellier's
Linkage - The Geometry Centre, University of Minnisota , US
Zie ook "Sylvester's rotator".
Zie ook "Cardio�des met stangenmechanisme".

[peaucel.htm] laatste wijziging op: 03-01-2003