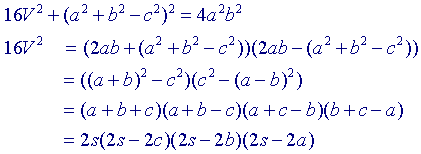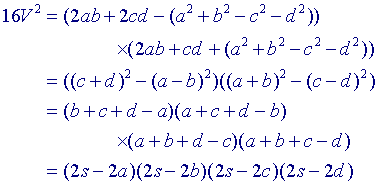De formule van Heron
Overzicht ][ Geschiedenis | Meetkunde
0. Overzicht
- Inleiding
- Heron's bewijs
- Twee andere bewijzen
3.1. Met incirkel en uitcirkel
3.2. Met goniometrie
- Oppervlakte van een vierhoek (Brahmagupta)
- Drie andere formules
- Tenslotte, drie cirkels
Zie ook het artikel Meetkunde, en wat inductie (met oa.
gebruik van de Formule van Heron). PDF-bestand (ca. 140 Kb / aug.2009)
1. Inleiding
Heron van Alexandri� (~10 - ~75, Egypte) schreef
onder meer een driedelig werk, Metrica, waarin oppervlakten van driehoeken,
vierhoeken, regelmatige veelhoeken, en inhouden van lichamen worden behandeld. Hij komt
daarbij ook tot benaderingen van wortels.
In Metrica, I-8, geeft hij de afleiding van de naar hem genoemde formule voor de
oppervlakte van een driehoek (uitgedrukt in de zijden van die driehoek):
V = �
s(s - a)(s - b)(s - c)
Hierin staat s voor de halve omtrek van de driehoek (dus 2s = a + b + c).
Overigens is uit Arabische bronnen bekend, dat de formule aan Archimedes moet worden
toegeschreven.
Als toepassing van de formule met wortelbenadering geeft Heron (Metrica, I-8;
in een vertaling van Th. Heath, A History of Greek Mathematics, vol. II, pagina
324) voor a = 7, b = 8 en c = 9 (waarbij dus V = �720):
Since 720 has not its side rational, we can obtain its
side within a very small difference as follows. Since the next succeeding square number is
729, which has 27 for its side, divide 720 by 27. This gives 26 2/3. Add 27 to this,
making 53 2/3, and take half this or 26 5/6. The side of 720 will therefore be very nearly
26 5/6. In fact, if we multiply 26 5/6 by itself, the product is 720 1/36, so the
difference in the square is 1/36.
If we desire to make the difference smaller still than 1/36, we shall take 720 1/36
instead of 729 (or rather we should take 26 5/6 instead of 27), and by proceeding in the
same way we shall find the resulting difference much less than 1/36.
2. Heron's bewijs
We geven hieronder Heron's bewijs van 'zijn' formule, waarbij we de tekst van Heath
volgen, daarbij echter gebruik makend van een modernere notatie (bijvoorbeeld: V(PQR) =
oppervlakte van driehoek PQR) en ietwat moderner woordgebruik.
| figuur 1 |
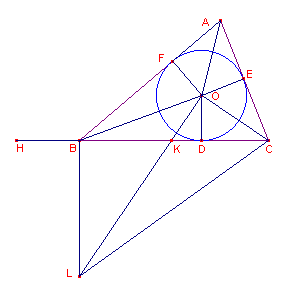 |
Laten de zijden van de driehoek ABC in lengte gegeven zijn (zie
figuur 1).
Teken de incirkel DEF met O als incentrum.
Dan is
BC.OD = 2V(BOC)
CA.OE = 2V(COA)
AB.OF = 2V(AOB)
Optelling geeft dan p.OD = 2V(ABC), waarin p de omtrek is.
Verleng nu CB naar H, zodat BH = AF.
Dan hebben we, omdat AE = AF, BF = BD en CE = CD,
CH = �p = s
Daarom is CH.OD = V(ABC), of ook
rs = V(ABC)
waarbij r de straal is van de incirkel. |
Teken nu OL loodrecht op OC en BL loodrecht op BC.
Nu is COBL een koordenvierhoek [dk: Thales-cirkel op CL].
Gevolg: hoek COB + hoek CLB = 180�.
Maar ook hoek COB + hoek AOF = 180�, omdat OA, OB, OC bissectrices zijn van de hoeken
rond O.
Gevolg: hoek AOF = hoek CLB.
De rechthoekige driehoeken AOF en CLB zijn dus gelijkvormig, waaruit
BC : BL = FA : FO = BH : OD
Waaruit weer
BC : BH = BL : OD = BK : DK [dk: immers OD // BL].
Dus
(BC + BH) : BH = (BK + DK) : DK of
CH : BH = BD : DK
Hieruit volgt weer [dk: door vermenigvuldiging van de elementen in het linker en rechter
lid]:
CH2 : (CH.BH) = (CD.BD) : (CD.DK).
Nu is CD.DK = r2, omdat driehoek ODC rechthoekig is, en CH = s, zodat
r2s2 = CH.BH.BD.CD
In onze moderne notatie, met V(ABC) = rs (zie boven):
V2 = s(s-a)(s-b)(s-c).
Zodat
V(ABC) = �
s(s - a)(s - b)(s - c)
�
3. Twee andere
bewijzen
3.1. Incirkel en uitcirkel
Het onderstaande bewijs, weliswaar ook gebaseerd op gelijkvormige driehoeken, verloopt
iets eenvoudiger dan het bewijs van Heron.
| figuur 2 |
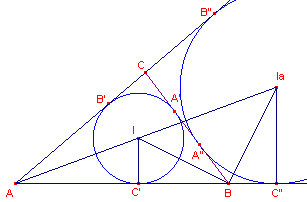 |
Wederom is (in figuur 2) de incirkel A'B"C'
getekend, met centrum I. Ook is de uitcirkel aan de zijde a getekend; middelpunt Ia
en straal ra.
Omdat de raaklijnstukken uit A, B, C aan de incirkel gelijk zijn, hebben we:
AB' + BC' + CB' = s.
Dus
BC' = s - b en (evenzo) ook AC' = s - a.
Op analoge wijze vinden we bij de uitcirkel:
AC" = s en BC" = s - c
Uit de gelijkvormigheid van de driehoeken AC'I en AC"Ia leiden we af:
IC' : IaC" = AC' : AC" |
Of
r : ra = (s - a) : s ...... (1)
De gelijkvormigheid van IC'B en BC"Ia levert"
IC' : BC" = BC' : IaC"
of
r : (s - c) = (s - b) : ra ...... (2)
Vermenigvuldiging van de leden van (1) en (2) geeft dan:
r2 : ra(s - c) = (s - a)(s - b) : sra
Zodat
r2s = (s - a)(s - b)(s - c)
waauit we vinden
r2s2 = s(s-a)(s-b)(s-c)
en dus met V(ABC) = rs (zie Heron's bewijs)
V(ABC) = �
s(s - a)(s - b)(s - c)
�
3.2. Met goniometrie
Bekend is dat voor een willkeurige driehoek ABC geldt
V(ABC) = �absinC
en
c2 = a2 + b2 - 2ab cosC (zie Cosinusregel)
(we geven de hoeken van de driehoek even aan met hoofdletters).
Eliminatie van C uit beide identiteiten met sin2C + cos2C = 1 geeft
dan:
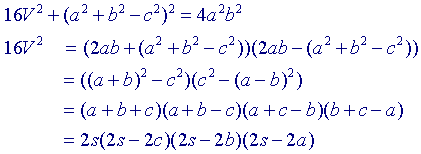
Waaruit dus volgt
V(ABC) = �
s(s - a)(s - b)(s - c)
�
Opmerkingen
[1]
Het formuledeel hierboven
16V2 + (a2 + b2-c2)2
= 4a2b2
geeft voor driehoek die in C rechthoekig is, samen met de oppervlakte waarvoor geldt dat V
= �ab:
4a2b2 + (a2 + b2-c2)2
= 4a2b2
waaruit dus volgt dat
a2 + b2 = c2
(Stelling van Pythagoras).
[2]
De formule van Heron kan ook worden gevonden door de driehoek op te vatten als een
"ontaarde" koordenvierhoek met een zijde met lengte 0.
Zie daarvoor paragraaf 4.
[einde Opmerking]
4. Oppervlakte van een vierhoek
Vermoedelijk door Brahmagupta (598-665, India) is de volgende eigenschap
ontdekt:
Voor de oppervlakte V van een koordenvierhoek met zijden a, b, c, d geldt:
V2 = (s - a)(s - b)(s - c)(s - d)
met 2s = a + b + c + d.
We gaan uit van de koordenvierhoek met oa. de hoekpunten E en F en zijden a, b, c, d (zie figuur 3).
| figuur 3 |
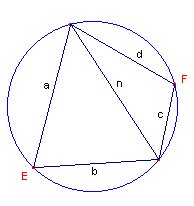 |
Omdat de hoeken E en F elkaars supplement zijn, geldt
cos E = - cos F
Volgens de cosinusregel is nu
n2 = a2 + b2 - 2ab cos E
n2 = c2 + d2 - 2cd cos F
waaruit we vinden:
2(ab + cd) cos E = a2 + b2 - c2 - d2
...... (1)
Voor de oppervlakte V van de koordenvierhoek hebben we:
V = �ab sin E + �cd sin F = �(ab + cd) sin E,
zodat
2(ab + cd) sin E = 4V ...... (2) |
Kwadratering van (1) en (2), gevolgd door optelling, levert dan
4(ab + cd)2 = (a2 + b2 - c2
- d2)2 + 16V2
of
16V2 = (2ab + 2cd)2 - (a2 + b2
- c2 - d2)2
We herleiden nu verder:
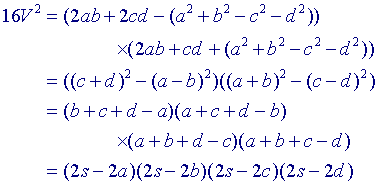
waaruit dus volgt
V2 = (s - a)(s - b)(s - c)(s - d)
�
Opmerking
Voor d = 0 hebben we dus de formule van Heron.
[einde Opmerking]
5. Drie andere formules
[1]
Uit V2 = s(s-a)(s-b)(s-c) = r2s2 volgt onmiddellijk
r2 = (V/s)2 = (s-a)(s-b)(s-c)/s
[2]
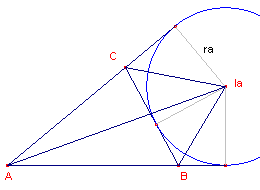
We kunnen ook een middelpunt van een uitcirkel gebruiken om de oppervlakte van ABC te
berekenen.
| V(ABC) |
= V(ABIa) + V(ACIa) - V(BCIa) |
|
= �cra + �bra - �ara = �(c+b-a)ra |
Zodat
V(ABC) = �(s-a)ra
Analoog geldt dus ook
V(ABC) = �(s-b)rb
V(ABC) = �(s-c)rc |
 |
[3]
We kunnen de stralen van de in- (r), uit- (ra, rb, rc) en
omgeschreven cirkel (R) van een driehoek met elkaar in verband brengen.
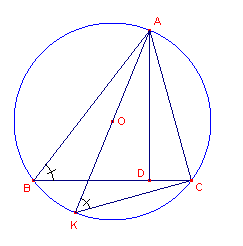
Uit de gelijkvormigheid van de driehoeken ABD en AKC
("Thales-driehoek") vinden we:
AB : AK = AD : AC
zodat
AD = (bc)/(2R)
Voor V = BC.AD/2 hebben we dan
V = (abc)/4R
of
| 4VR |
= abc = (herschrijven) |
|
= -(s-a)(s-b)(s-c) + s(s-b)(s-c) + s(s-a)(s-c) + s(s-a)(s-b) |
|
= -V2/s + V2/(s-a) + V2/(s-b) + V2/(s-c) |
|
=V(-r + ra + rb + rc) |
Dus:
4R = (ra + rb + rc - r) |
 |
6. Tenslotte, drie cirkels
Een eenvoudige uitdrukking van de formule van Heron kan worden verkregen,
als we gebruik maken van de stralen van de drie cirkels (met de hoekpunten als middelpunt)
die door de raakpunten van de incirkel aan de zijden gaan (zie figuur 4).
| figuur 4 |
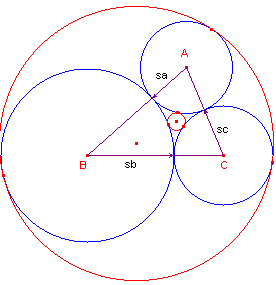 |
De stralen van deze cirkels zijn opvolgend sa, sb,
sc.
We hebben nu
a = sb + sc
b = sc + sa
c = sa + sb
Nu is s =�(a + b + c) = sa + sb + sc
en verder
s - a = sa, s - b = sb, s - c = sc
Zodat
V2 = sasbsc(sa+sb+sc) |
Opmerking
Bovenstaande configuratie, de drie cirkels door de raakpunten van de incirkel, bepalen de
beide zogenoemde Soddy-cirkels (deze zijn eveneens getekend in figuur 4). De Soddy-cirkels raken de "hoekpunts"-cirkels in- en
uitwendig.
Zie ook de pagina "Soddy-cirkels".
[einde Opmerking]

[heron.html] laatste wijziging op: 21-07-10 (07-04-2005)