Bollen van Dandelin
Dandelin | Ellips
| Parabool | Hyperbool | Referenties ][ Analytische
meetkunde
1. De stelling van Dandelin

Germinal Pierre Dandelin (1794-1847, Le Bourget) werd geboren in
Frankrijk, maar wordt toch beschouwd als Belgisch wiskundige; hij bracht het grootste deel
van zijn leven in Belgi� door (zijn moeder was Belgische), maar zeker ook omdat hij enige
tijd mijnbouwkunde doceerde aan de universiteit van Luik.
Dandelin's eerste wiskundige belangstelling gold de meetkunde.
In 1822 ontdekte hij een belangrijke stelling, naar hem genoemd, over het verband tussen
de doorsnede van een vlak en een kegel, en binnen die kegel beschreven bollen, de
bollen van Dandelin.
De stelling van Dandelin en de genoemde bollen worden behandeld in de paragraaf
2 (ellips), paragraaf 3 (parabool) en paragraaf 4
(hyperbool).
| figuur 1 |
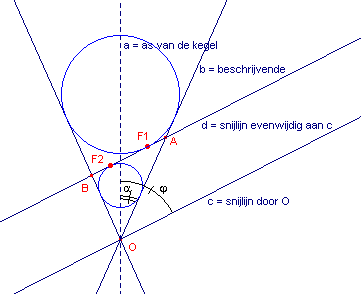 |
In figuur 1 is een doorsnede getekend van een kegel met het vlak van
tekening T (diagonaalvlak).
a is de as van de kegel en b is een beschrijvende.
a is de halve tophoek van de kegel.
c is de snijlijn van een vlak door O loodrecht op T. Dit vlak maakt met de as van de kegel
een hoek j die groter is dan a.
d is de snijlijn van een vlak dat evenwijdig is aan het vlak door O.
Dit vlak snijdt de in het diagonaalvlak gelegen beschrijvenden van de kegel in de punten A
en B.
De punten F1 en F2 zijn de raakpunten van de bollen van
Dandelin aan het snijvlak.
De doorsneden van deze bollen met het diagonaalvlak zijn de incirkel van driehoek OAB en
de aancirkel van die driehoek aan de zijde AB. |
Klik hier  voor een animatie van het bovenstaande met CabriJava. voor een animatie van het bovenstaande met CabriJava.
|
| 2. Ellips |
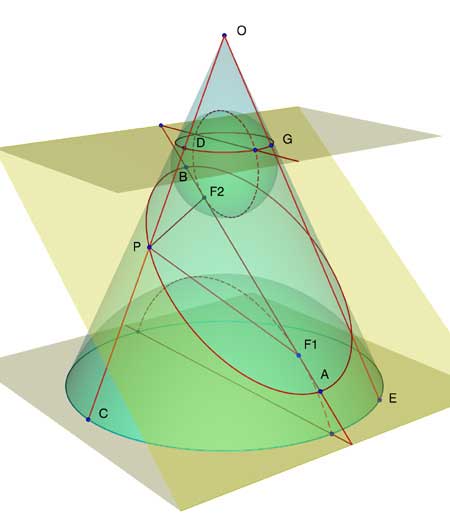 |
In deze figuur links maakt het snijvlak een hoek j met
de as van de kegel waarbij j > a
(zie ook figuur 1). P is een punt van de doorsnede van het vlak
en de kegel.
F1 en F2 zijn de raakpunten van de bollen van Dandelin aan dat vlak.
De beschrijvende van de kegel die door P gaat (PO), raakt eveneens aan deze bollen (in de
punten C en D).
De raaklijnstukken uit een punt aan een bol zijn gelijk. Dus
PC = PF1 en PD = PF2.
Zodat
PF1 + PF2 = PC + PD = CD
F1 en F2 zijn vaste punten van het snijvlak.
De afstand CD = EG is constant.
De som van de afstanden van de punten van de snijkromme is dus constant.
De snijkromme van het vlak en de kegel is dus een ellips. |
Zie ook de Opmerking over de richtlijnen na paragraaf 4.
| 3. Parabool |
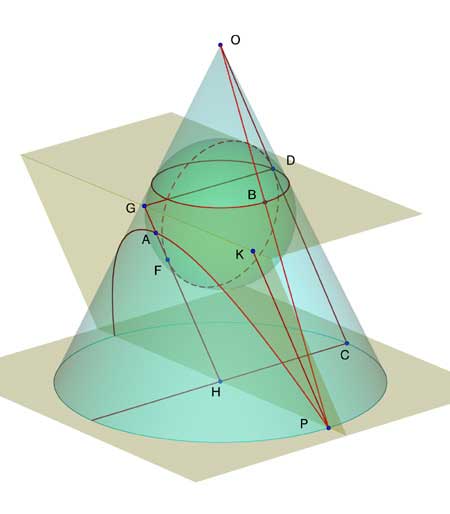 |
In de figuur hiernaast is een snijvlak getekend waarvoor geldt j = a. Er is nu slechts ��n
bol van Dandelin die vlak en kegel raakt.
Zij P een punt van de doorsnede. P wordt verbonden met het raakpunt F en met O.
PF en PB (B op PO) zijn dan raaklijnstukken aan de bol. Dus PF = PB.
Zij CP de parallelcirkel van P. Dan is PB = CD.
Nu is CHGD een parallellogram, zodat CD = HG.
We beschouwen nu de snijlijn van het vlak waarin de parallelcirkel BD is, met het
snijvlak.
PK is de loodlijn uit P op deze snijlijn.
Nu is, omdat KPKG een rechthoek is, PK = HG.
Samenvattend:
PF = PB = CD = HG = PK.
Voor een punt van de doorsnede geldt dus dat de afstand daarvan tot F gelijk is aan de
afstand tot een vaste lijn.
De doorsnede is dus een parabool. |
Zie ook de Opmerking over de richtlijn na paragraaf 4.
| 4. Hyperbool |
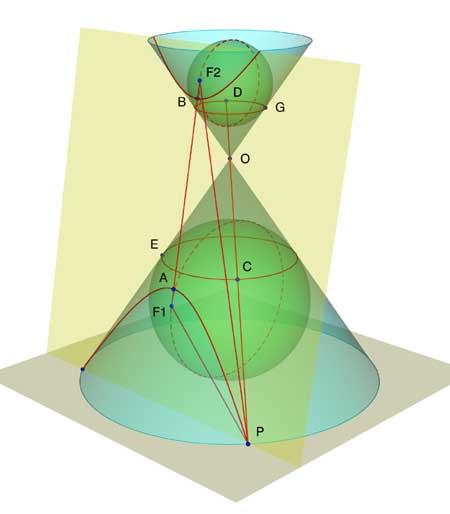 |
In nevenstaande figuur is een snijvlak getekend waarvoor j < a. In dit geval snijdt
het vlak de beide bladen van de kegel.
Kiezen we P nu op ��n van de "takken" van de doorsneden.
F1 en F2 zijn weer de raakpunten van de bollen van Dandelin met het
snijvlak.
De beschrijvende door P raakt eveneens aan deze bollen (in de punten C en D), zodat
PF1 = PC en PF2 = PD.
We hebben nu
PF2 - PF1 = PD - PC = CD.
Het lijnstuk CD (= EG) is constant; het is het deel van de beschrijvende tussen de beide
parallelvlakken (waarin de parallelcirkels BG en CE gelegen zijn).
Omdat nu het verschil tussen de afstanden van P tot de raakpunten constant is, ligt P dus
op een hyperbool
Zie ook de Opmerking over de richtlijnen. |
Opmerking over de richtlijnen
De snijlijnen van de vlakken (bij de parabool: de snijlijn van het vlak) waarin de
raakcirkels van de bollen met de kegel liggen, met het vlak waarin de kegelsnede ligt,
zijn de richtlijnen van de kegelsnede (zie ook de pagina "Kegelsneden en hun vergelijkingen")..
De "doorgangen" van de richtlijnen kunnen in de CabriJava-animatie
worden zichtbaar gemaakt
[Einde Opmerking]
5. Referenties
Als ontdekker der kegelsneden wordt gewoonlijk Menaechmus (~380-~320 vC), vermoedelijk leerling van Eudoxos, genoemd. Euclides moet ook een boek
over kegelsneden hebben geschreven, dat verloren is gegaan. Men draagt er alleen kennis
van door mededelingen van latere wiskundigen, daar Euclides in zijn overige werken slechts
een enkele maal over kegelsneden spreekt.
Het belangrijkste werk is dat van Apollonius van Perga.
Verder:
[1] Dr. D.J.E. Schrek, Beknopte analytische meetkunde, P. Noordhoff, Groningen,
1964
[2] Webpagina "Kegelsneden als doorsnede", een animatie
[3] Webpagina "Kegelsneden en hun vergelijkingen
[4] Webpagina "Pooltransformaties"

De illustaties in de paragrafen 2, 3 en 4 zijn vervaardigd door
K e e s
B o e r
Zamenhoflaan 9
3411 ZV LOPIK |
|
tel.: 0348 550660
fax.: 0348 550666
e-mail: info@3demo.nl |
|
 |
[dandelin.htm] laatste wijziging op: 08-08-2004




