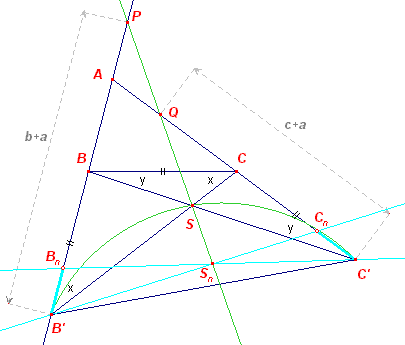
Zij S nu het snijpunt van B'C en C'B als ABC de gezochte driehoek is.
Is verder BB'C = x en CC'B = y, dan is ook:
A + B + C = 180, B = 2x (buitenhoek van BB'C), C = 2y (buitenhoek van
CC'B)
Zodat A = 180 - 2x - 2y, of �A = 90 - x - y
Voor B'SC' hebben we dan (in BSC):
B'SC' = 180 - x - y = 90 + (90 - x - y) =
90 + � A.
De meetkundige plaats van het punt S is daardoor bekend (stelling van de omtrekshoek): een
cirkelboog.
We kiezen nu op B'A en C'A opvolgend de punten Bn en Cn, met B'Bn
= C'Cn.
Deze punten vormen twee projectieve puntreeksen.
De stralenbundels van de lijnen B'Cn en C'Bn zijn dus eveneens
projectief.
Echter B'C' is een gemeenschappelijke straal van deze bundels, waaruit volgt dat de
bundels perspectief zijn.
De snijpunten, Sn, van overeenkomstige stralen zijn daardoor collineair.
De collineatie-as is de lijn PQ in nevenstaande figuur.