Probleemstelling | Oplossing | Bewijs | Naschrift ][ Inversie | Meetkunde
Zie ook het Cabri-werkblad "Kijkhoek".
| figuur 1 | 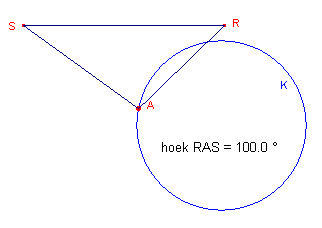 |
Gegeven zijn een lijnstuk RS en een cirkel K. Op K ligt een punt A. Construeer de posities van A op K, waarvoor de "kijkhoek" RAS maximaal en minimaal is. Opmerking |
Klik hier ![]() voor een CabriJavapplet
bij deze probleemstelling.
voor een CabriJavapplet
bij deze probleemstelling.
| figuur 2 | 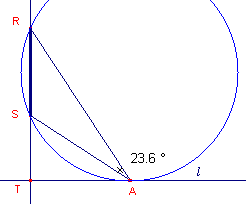 |
Het probleem is een algemenisering van het geval waarbij het punt A op
een rechte lijn ligt. Immers een rechte lijn is een cirkel met oneindig grote straal. En hierin ligt dan tevens de oplossing. Via inversie ten opzichte van een geschikt gekozen cirkel kan K worden afgebeeld op een rechte lijn. De maximale kijkhoek wordt in dat geval gevonden als het punt A het raakpunt is op de rechte lijn (K') van de cirkel door R en S (zie figuur 2, waarin l = K'). |
Een gelukkige, maar noodzakelijke, bijkomstigheid is dat relaties tussen hoeken invariant zijn bij inversie.
| figuur 3 | 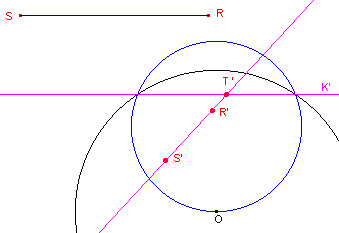 |
In nevenstaande figuur zijn de eerste transformaties uitgevoerd. O (gelegen op K) is middelpunt van de inversiecirkel (met willkeurige straal). R' en S' zijn de beelden van R en S bij deze inversie ; K' (een rechte lijn) is het beeld van K. T' is het snijpunt van K' en de lijn R'S'. We moeten nu de cirkel door R' en S'
construeren die raakt aan de lijn K' (zie daarvoor het Cabri-werkblad "Kijkhoek" of de pagina "Maximale
kijkhoek"). |
| figuur 4 | 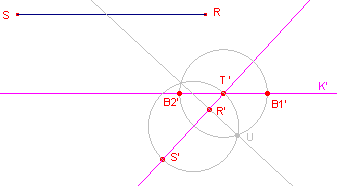 |
In figuur 4 is deze constructie uitgevoerd. Allereerst is de cirkel met
middellijn T'S' getekend. |
| figuur 5 | 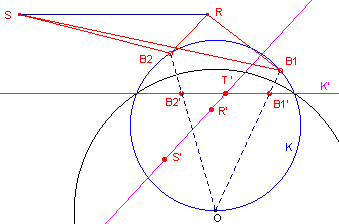 |
Wanneer we "teruginverteren" krijgen we de
punten B1 en B2 (gelegen op K) die de
gezochte punten zijn. Zie figuur 5, waarin: |
Dat in B1 een minimum, en in B2 een maximum waarde wordt gevonden, "zien" we uit de tekening. Een bewijs daarvoor staat hieronder.
| figuur 6 | 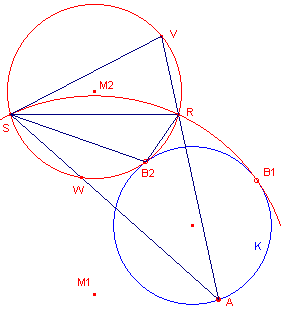 |
De punten B1' en B2'
zijn de raakpunten op de lijn K' van cirkels door R' en S'. Bij "teruginversie" gaan die cirkels over in cirkels (met middelpunten M1 en M2) door R en S die in B1 en B2 raken aan K. In B2 raakt cirkel M2 uitwendig aan K; in B1 raakt cirkel M1 inwendig aan K. Voor het punt A op K hebben we dan, kijkend naar bogen op cirkel M2:
Zodat hoek RAS < hoek RB2S. |
Naschrift ![]()
Op de pagina "Beweging en
Optimalisering" van de website
van Henk Pfaltzgraff staat een programma voor de TI83 (grafische rekenmachine) waarmee
berekeningen bij dit probleem kunnen worden uitgevoerd.
[maxhoekcirk.htm] laatste wijziging op: 16-03-01