• Een busmaatschappij
       Bij vraag d
       Bij vraag e
       Bij vraag f
• Download

1	De busmaatschappij heeft elk jaar 90 miljoen gulden nodig voor investeringen.
2	q is het aantal passagiers per jaar in miljoenen.
3	Het aantal personeelsleden dat nodig is voor het vervoer van q miljoen passagiers, is gelijk aan.
4	Een personeelslid kost het bedrijf (gemiddeld) 100.000 gulden per jaar.
5	De gemiddelde ritprijs is 4 gulden per passagier.

De kostenfunctie, dat is de formule waarmee je de kosten K van het bedrijf per jaar kunt uitrekenen, is
.
Hierbij wordt K uitgedrukt in miljoenen guldens.

a.	Leg uit dat uit de gegevens volgt, dat de personeelskosten miljoen gulden per jaar zijn.
b.	In 1994 waren er 25 miljoen passagiers. Wat waren de kosten in dat jaar? Wat was de opbrengst in dat jaar? Was er sprake van winst of verlies voor de maatschappij? En hoeveel was dat?
c.	Leg uit dat voor de opbrengst O in het algemeen geldt, dat O(q) = 4q. Hierbij wordt O uitgedrukt in miljoenen guldens.
d.	Plot de grafieken van K en O in ��n assenstelsel. Zoek daarna uit voor welke waarde(n) van q de busmaatschappij winst maakt. Zie toelichting
e.	Gebruik de plot voor een schatting van de waarde van q waarvoor de winst van de busmaatschappij maximaal is. Zie toelichting
f.	Stel een functie (formule) op voor de winst W. Dus W(q) = … Bereken de maximale winst. Zie toelichting

De functie K(q) schrijven we dus als en de functie O(q) als O(x) = 4x. Voer de functies K en O nu in via het [Y=] scherm. (>>>)

Voordat je de grafieken gaat plotten, zeker als je uit de grafiek gegevens moet aflezen (zie vraag e), is het zaak je af te vragen welke intervallen voor x en y je moet gebruiken.

De instellingen daarvan vind je in het [WINDOW]-menu van de GR. Meestal kan je deze instellingen afleiden uit eerder beantwoorde vragen. Zie bijvoorbeeld vraag b, waarin je de waarde van K hebt uitgerekend voor x = 25 (waarde 105,6). Kies daarom voor x waarden tussen 1 en 50 en voor y waarden tussen 1 en 150.

Voor welke waarden van x (dat zijn ook de waarden van q) snijden de grafieken K en O elkaar?
Gebruik hierbij de [TRACE]-functie van de GR.

Bereken de waarden van K en O voor x = 27,06.
Wat is de betekenis van deze waarde van q in termen van winst en verlies voor de busmaatschappij?
Bepaal (bereken) ook een tweede waarde van x waarvoor K(x) en O(x) gelijke waarden hebben.
Aanwijzing
[1]
Vergroot de waarden van Xmax en Ymax in het [WINDOW]-menu van de GR zo, dat de beide snijpunten van de grafieken in het grafisch venster zichtbaar zijn en gebruik dan opnieuw de [TRACE]-functie.
[2]
Je kunt ook de vergelijking
   of
oplossen met behulp van de abc-formule.

Bereken de winst voor de waarden q = 79, q= 80 en q = 81.
Hoe kan je deze waarden van q uit de grafiek van K en O afleiden?

Bedenk, dat de winst wordt berekend door de opbrengst te verminderen met de kosten. Je kan de winstfunctie ook invoeren in het [Y=]-scherm (zie Y3).

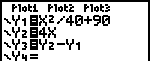Als je daarna de drie grafieken plot, dan krijg je iets als (>>>)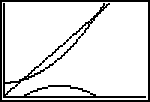

Wat is de naam (het type) van de grafiek van de winstfunctie?
Waar vind je het maximum van een dergelijke functie?
Aanwijzing
Gebruik opnieuw de [TRACE]-functie.

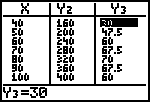
Je kan nu erg goed gebruik maken van de [TABLE]-functie van de GR om de maximale waarde van de winst te laten berekenen. Gebruik daarbij het [TBLSET]-menu voor de instellingen. Natuurlijk moet je de maximale waarde van de winst ook kunnen bepalen via de formule van de winstfunctie. Doe dat dus, want dat is eigenlijk de vraag.

Download
Dit werkblad kan via deze website worden gedownload. Het is alleen beschikbaar in PDF-formaat.
Een PDF-bestand kan met Acrobat^� Reader worden gelezen:

mwa11-60.pdf [15Kb]

[mw1160.htm] laatste wijziging op: 28-01-2000