Overzicht - bij Moderne Wiskunde A1, deel 1 (VWO) - Hoofdstuk A1, Extra A (pag. 36)
Opgave A1
De firma Zellerman BV produceert fietsen.
Als in een maand q fietsen worden geproduceerd, dan zijn in die maand de gemiddelde
kosten:
![]() .
.
| a. | Onderzoek de bijzonderheden van de grafiek van deze formule
en maak een schets (op papier dus). Zie toelichting |
| b. | De fabrikant wil de gemiddelde kosten per fiets zo
klein mogelijk houden. Naar welke maandproductie zal hij streven? Zie toelichting |
| c. | Door een staking ligt de productie aan maand lang stil. Wat gebeurt er dan met de gemiddelde kosten in die maand? Hoe kan je dat zien aan de formule? |
| d. | Onderzoek bij welke waarden van q de gemiddelde kosten
minder dan f 350,- zijn. Zie toelichting |
| e. | Bereken de totale kosten bij een maandproductie van 5000 fietsen. |
| f. | Stel een formule op voor de totale kosten TK. Dus TK = … |
Bij opdracht a.
| Je kunt natuurlijk een plot van de grafiek maken. Daarbij
moet je bedenken, dat de GR op de horizontale as gebruik maakt van de variabele x. We hebben dus te maken met de functie We leggen de functie op de GR vast met [Y=]. (>>>) |
Je moet natuurlijk ook zinvolle waarden nemen voor x.
Als je het vraagstuk doorleest tot het eind, dan kan je in dit geval zien (vraag e), dat
in waarden van enkele duizenden stuks moet worden gerekend.
Stel dus de waarden in het [WINDOW]-menu in op bijvoorbeeld Xmin = 0 en
Xmax = 10 000. Geef ook Xscl (de schaal van X) een aangepaste waarde (dus
niet gelijk aan 1).
| Ook de waarden van Ymin en Ymax (en eventueel ook Yscl) moet
je aanpassen. Berekening van bijvoorbeeld GK(3000) geeft ƒ 341,67. Je kan dan een grafiek krijgen als hiernaast. (>>>) |
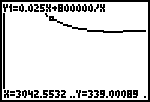 |
Het is verstandig te experimenteren met de waardes van Ymin en Ymax om een goed beeld
van het verloop van de functie te krijgen.
In het hierboven staande geval is het aan te bevelen de waarde van Xmax te vergroten,
waardoor beter inzicht wordt verkregen in de verloop van de functie voor grotere waarden
van x.
Bij opdracht b.
| Je kan ook gebruik maken van de [TABLE]-functie. Hiernaast staat een schermafdruk. (>>>) |
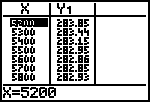 |
| Je kan een betere benadering van de de minimale waarde
verkrijgen door de instellingen van de tabel te wijzigen in het
[TBLSET]-menu.(>>>) Gebruik dan een kleinere waarde voor D Tbl. |
 |
Bij opdracht d.
| Je kan ook een tweede functie (die voor de constante waarde 350) met [Y=] vastleggen en daarna de beide functies plotten. | 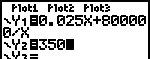 |
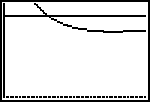
| Voor een juiste plot van de beide grafieken (zie figuur
hiernaast) is aanpassing van de instellingen in het [WINDOW]-menu wel nodig, immers er
zijn twee snijpunten (waarom?), en er is er slechts ��n zichtbaar. Bepaal daarna met
de [TRACE]-functie de snijpunten van de functies Y1 en Y2. |
 |
| a. | In januari worden 6000 dozen geproduceerd, in februari 5500. Bereken voor beide maanden de totale kosten en ook de gemiddelde kosten per doos. |
| b. | Waarom zijn de gemiddelde kosten per doos in januari lager dan die in februari? |
We noemen TK de totale kosten per maand, en q het aantal dozen dat in een maand geproduceerd wordt.
| c. | Stel een formule op voor TK als functie van q. |
| d. | Stel ook een formule op voor de gemiddelde kosten GK per doos. |
| e. | Hoe kan je aan de formule voor GK zien, dat de gemiddelde kosten dalen naarmate q groter wordt? |
| f. | Plot de grafiek van de functie GK en geef daarna een
schets van de grafiek. Tot welk getal nadert GK als q steeds groter wordt? Zie toelichting |
Bij opdracht f.
| Leg de gevonden functie voor TK vast achter Y1 met [Y=]. Ga na dat in de hiernaast staande schermafdruk het functievoorschrift voor de gemiddelde kosten GK is vastgelegd achter Y2. |
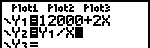 |
Is het mogelijk de functies GK en TK beide tegelijk (dwz. in
hetzelfde scherm) te plotten?
Verklaar je antwoord.
Download
Dit werkblad kan via deze website worden gedownload. Het is alleen
beschikbaar in PDF-formaat.
Een PDF-bestand kan met Acrobat� Reader
worden gelezen: ![]()
![]() mwa11-36.pdf [16Kb]
mwa11-36.pdf [16Kb]
[mw1136.htm] laatste wijziging op: 28-01-2000