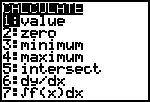
Het commando is als 1:value te vinden in het menu CALCULATE. [CALC] is als toets te vinden op de bovenste rij knoppen van de GR.
1. Snijpunt met de y-as, andere
functiewaarden
We gaan uit van de functie
f(x) = 3x2 - 2x - 2.
Het snijpunt van een grafiek met de y-as vinden we voor x = 0.
In de gegeven functie geeft dit f(0) = 0 - 0 - 2 = -2.
De co�rdinaten van het snijpunt zijn dus (0; -2).
We hebben dus voor een bepaalde waarde van x de bijbehorende y-waarde
berekend.
De GR kent hiervoor een speciale opdracht (commando), die we dus ook voor het bovenstaande
kunnen gebruiken.
| Maar ook bij andere waarden van x kunnen we met die
opdracht de bijbehorende waarde van y berekenen. Het commando is als 1:value te vinden in het menu CALCULATE. [CALC] is als toets te vinden op de bovenste rij knoppen van de GR. |
 |
| Voorwaarde voor het gebruik van commando’s in CALCULATE is, dat de te onderzoeken functie(s) in het grafische scherm zichtbaar zijn. | |
We moeten dus eerst via [Y=]
het functievoorschrift vastleggen.
Wis de eventueel daarin staande voorschriften met [CLEAR]
.
Doe dat dus voor elke Y!
| Leg dan het voorschrift f(x) = 3x2 - 2x - 2 vast (gebruik de toets [X,T,..] voor de X). | 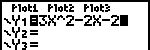 |
| Selecteer nu de grafiek via het grafische scherm (met [GRAPH] ). Kies via het ZOOM-menu bijvoorbeeld 4:Zdecimal. |
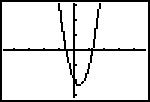 |
Eerst nu kunnen we gebruik maken van het commando 1:value in het CALC-menu.
| Druk dus op [CALC]
[ 1 ] . Je ziet dan, dat de machine gereed is om een x-waarde te ontvangen (onderin het scherm). |
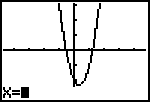 |
| Druk dan op [ 0 ],
gevolg door [ENTER]. In het scherm worden dan het functievoorschrift (Y1=...) en de berekende y-waarde zichtbaar (de laatste rechtsonder in het scherm). Inderdaad, ook de GR vindt het punt (0; -2); zie ook het punt op de grafiek. |
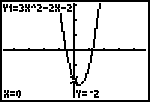 |
Om de y-waarde bij een andere waarde van x te berekenen moeten we opnieuw gebruik maken van het CALC-menu.
- Bereken nu f(1,38); f(-0,4) en f(4,5).
- Bereken ook f(5) en f(100).
| Hierbij kunnen foutmeldingen optreden omdat de gekozen
waarde van x buiten de grenzen van het scherm valt. Als je dan op 2:Goto drukt, kom je weer in het grafische scherm en kan je (eventueel met gebruik van de [DEL]-toets) een nieuwe waarde voor x invoeren. |
2. Gebruik van de variabelen Y1, ...
| Verlaat het grafische scherm met [QUIT] en kies [VARS] <Y-VARS>. |  |
| Met dit menu kan je de functievariable Y1 kiezen. Druk op 1:Function. Je krijgt dan een lijst met de namen. |
|
| Druk dan op 1:Y1. De naam van deze variabele wordt hiermee naar het basisscherm gekopieerd. |
|
| We kunnen nu de waarde van x tussen haakjes
"meegeven" als bijvoorbeeld Y1(100). De haakjes moet je dus zelf plaatsen! |
|
| Na het drukken op [ENTER] wordt de functiewaarde uitgerekend. |
| Bereken voor x = -10 tot en met x = 10
(stapjes van 1) de functiewaarden van de functie f(x) = 3,1x2 + 2,9x - 32,5. Zet de waarden (afgerond op drie decimalen) op papier in een (horizontale) tabel. Maak ook een schets van de grafiek. |
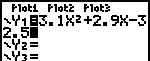 |
Aanwijzing
We kunnen de nulpunten gemakkelijk met de GR bepalen (eigenlijk moeten we spreken van benaderen).
We doen dat in deze paragraaf voor de functie
f(x) = 3x2 - 2x -
2.
Ook nu is het noodzakelijk, dat de grafiek op het grafische scherm staat.
Daarnaast moet ten minste ��n de snijpunten van de grafiek met de x-as op het
scherm zichtbaar zijn.
| Kies nu weer [CALC] en in dat menu de opdracht 2:zero. | 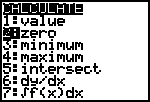 |
| We zien dan op het scherm, links onderaan Left bound? Hiermee wordt de linker grens van het interval aangewezen, waarbinnen het gezochte nulpunt moet liggen. |
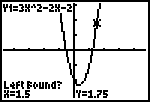 |
We moeten nu het punt (de cursor) op de grafiek zo verplaatsen, dat het links van het
gezocht nulpunt komt te liggen.
Gebruik hiervoor de knoppen [�]
en/of [�].
| Als eerste zoeken we bij de genoemde functie het nulpunt op
de positieve x-as. Als de cursor op de grafiek links van dat nulpunt ligt, druk dan op [ENTER] . Op het scherm wordt de linker grens van het interval nu aangegeven met een driehoekje. Tegelijk zien we uit Right bound? dat we nu de rechter grens van het interval moeten vastleggen. |
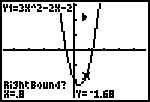 |
Verplaats nu het punt op de grafiek naar een positie rechts van het gezochte nulpunt. En druk weer op [ENTER] .
| De aanwijzer (weer een driehoekje) in het grafische
scherm geeft dan de rechter grens van het interval aan. Op het scherm staat dan links onder Guess? Hiermee moet een punt geselecteerd worden dat dichtbij het gezocht nulpunt ligt, en tussen de beide grenzen. Druk daarna op [ENTER] . |
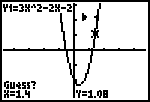 |
De GR benadert nu het gezocht nulpunt.
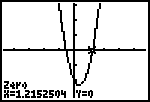
| De x-waarde (en de y-waarde) verschijnen daarna
op het scherm. Het beweegbare punt staat dan op het gezochte nulpunt. In dit geval is dat dus x = 1,215 (afgerond). |
 |
|
| Benader de nulpunten van de functie f(x) = 3,1x2 + 2,9x - 32,5 in drie decimalen nauwkeurig (dat wil zeggen, afgerond en geschreven met drie cijfers achter de komma). |
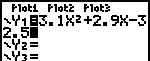 |
| We gaan nu uit van de functies f(x) = x2 - 2x - 2 g(x) = �x - 1 |
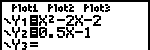 |
| Als we de grafieken van beide functies ( met s ) in ��n figuur weergeven, dan zien we dat ze elkaar in twee punten snijden. | 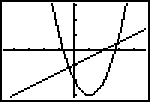 |
We vragen nu natuurlijk naar de co�rdinaten van die snijpunten.
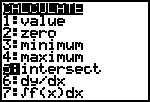
| Ook nu vinden we in het CALC-menu een commando dat de
benadering voor ons kan uitvoeren: 5:intersect (van het Engelse intersection). Druk dus op [ 5 ]. |
 |
We moeten nu de lijnen (curve) selecteren waarvan we de snijpunten willen benaderen.
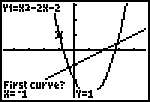
| We zien links onderaan eerst First curve? De cursor staat nu op ��n van beide grafieken. Druk op [ENTER], waarmee de eerste functie geselecteerd is (die wordt aangegeven met een + op de grafiek). |
 |
Onderaan links verschijnt nu Second curve?
Druk, indien nodig, op } of † om de cursor te laten verspringen naar de tweede
functie en druk op � .
Onderaan links staat nu Guess? De beide geselecteerde functies zijn aangegeven met een +.
Druk nu op [�] of [�] om de cursor te verplaatsen naar
een punt dichtbij het snijpunt van de beide grafieken.
Dit x-waarde van dat punt (dichtbij het snijpunt) heet wel testwaarde. Druk
weer op [ENTER].
Hierna wordt de benadering uitgevoerd.
| Voor het linker snijpunt hebben we dus gevonden: (-0,351; -1,175). | 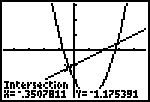 |
|
| Gegeven zijn de functies f(x) = x2 - 2x - 2 g(x) = -1/2x2 +2� Benader de co�rdinaten van de snijpunten van beide grafieken. |
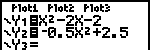 |
| Gegeven is de functie |
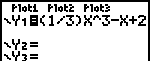 |
Opdracht 5
| Gegeven is de functie |
 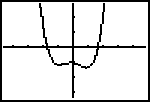 |
Aanwijzing
Gebruik zo nodig het commando [ZOOM]
1:Zbox.om de nulpunten en de extremen beter (groter) op het grafische scherm weer
te geven.
[calc83.htm] laatste wijziging op: 27-12-2004