Stelling 3 - Lijn van Steiner
Bewijs ][ Lijn van Steiner | DK & Meetkunde
Bewijs
We willen dus bewijzen:
Stelling
Het spiegelbeeld van het brandpunt
van een parabool in een raaklijn aan die parabool ligt op
de richtlijn van die parabool. |
Bewijs:
We bewijzen de stelling in de omgekeerde richting (zie figuur 1).
| figuur 1 |
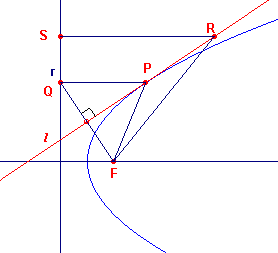 |
We verbinden het punt P met het
brandpunt F en trekken de lijn PQ loodrecht op de
richtlijn r. Uit de definitie van de parabool
weten we nu, dat PF = PQ.
We bewijzen nu, dat de middelloodlijn l van FQ
de raaklijn is in het punt P.We nemen nu aan, dat de
lijn l de parabool in een tweede punt R (dat dus
verschillend is van P) snijdt (in de figuur ligt P niet
op de parabool!)
Dat l raaklijn is volgt uit de overweging, dat
nu voor R geldt:
RF = RQ immers R ligt op de middelloodlijn
van FQ.
Maar RQ > RS (in een rechthoekige driehoek). We hebben
dus een tegenspraak!
R ligt dus niet op de parabool.
Dus l is raaklijn aan de parabool. ?
|
Opmerking
Op de in het bewijs aangegeven manier kunnen we dus bij gegeven
brandpunt en richtlijn op eenvoudige wijze de raaklijn in een
punt van een parabool construeren.
[einde Opmerking]
Terug naar de tekst

[steiner3.htm]
laatste wijziging op: 23-03-1999
