 |
De Vensters van Viviani
"Maak vier gelijkvormige vensters in een halve bol, zodanig dat het overblijvende bolstuk kwadreerbaar is." (Aenigma geometricum de miro opificio Testudinis Quadrabilis Hemisphaericae)
Kwadreerbaar betekent dat je de oppervlakte bij gegeven straal van de halve bol met passer en liniaal moet kunnen construeren.
Het is een pseudo-architectonisch probleem: de oppervlaktebepaling van een koepelgewelf.
 |
Tekening van het koepelgewelf van de San Fedele in Milaan |
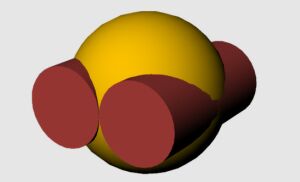
Viviani loste het probleem op door de halve bol te doorsnijden met twee halve
cilinders. Het oppervlaktestuk boven de cilinders noemde hij Vela Quadrabile
Fiorentina.
In Rhino heet deze bewerking: Boolean difference.
Hieronder is een en ander (deels) weergegeven met behulp van een gehele bol.
De gemeenschappelijke (snij)kromme is een ruimtekromme in de vorm van twee 8-en
(gelegen op de bol). Zo'n achtje heet "kromme van Viviani".
 |
 |
 |
Er geldt: Oppervlakte "vela" De oppervlakte is dus onafhankelijk van p. |