Regelmatige veelvlakken

Overzicht

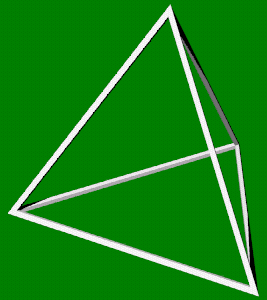
4 hoekpunten
6 ribben
4 zijvlakken (driehoek)
3 vlakken in een hoekpunt

6 hoekpunten
12 ribben
8 zijvlakken (driehoek)
4 vlakken in een hoekpunt

12 hoekpunten
30 ribben
20 zijvlakken (driehoek)
5 vlakken in een hoekpunt

8 hoekpunten
12 ribben
6 zijvlakken (vierkant)
3 vlakken in een hoekpunt

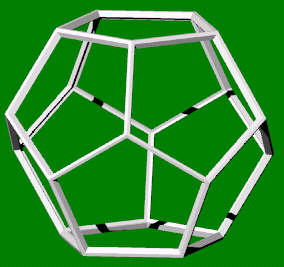
20 hoekpunten
30 ribben
12 zijvlakken (vijfhoek)
3 vlakken in een hoekpunt

Dit hangt samen met het aantal zijvlakken dat in hetzelfde hoekpunt samenkomt.
De som van de hoeken daar moet kleiner zijn dan 360�, want anders zouden de zijvlakken in hetzelfde vlak liggen (of "uitsteken").
Verder moeten in elk hoekpunt minstens 3 vlakken samenkomen. Elke vlakhoek moet dus kleiner zijn dan 360�/3 = 120�.
Er komen dus slechts drie-, vier- en vijfhoeken als zijvlak in aanmerking.
De hoek van een vijfhoek is gelijk aan 108�. Vier zijvlakken met een vijfhoek kan niet.
Er is dus slechts 1 regelmatig veelvlak (mogelijk) met een vijfhoek als "bouwsteen".
De hoek van een vierkant is 90�. Ook hier zijn vier zijvlakken onmogelijk.
Er is dus slechts 1 regelmatig veelvlak (mogelijk) met een vierkant als "bouwsteen".
Voor de driehoek hebben we:
3 x 60 = 180�; 4 x 60 = 240�; 5 x 60 = 300�.
Er zijn dus 3 regelmatige veelvlakken (mogelijk) met een driehoek als "bouwsteen".
En dat deze vijf er inderdaad ook zijn, zien we hierboven.