Moebius-band

M�bius-band

figuur a
moebius1.gif (1304 bytes)

figuur b
moebius2.gif (14919 bytes)

Plakken we van een strook papier de uiteinden (gewoon) aan elkaar dan ontstaat een ring met ��n binnenkant en een buitenkant.
Wanneer we, voordat we de uiteinden aan elkaar plakken, eerst ��n van de uiteinden een slag draaien ontstaat een zogenoemde M�bius-band.
Omdat nu de binnen- en de buitenkant in elkaar over gaan, blijft er dus maar ��n kant over.

Wiskundig gezien kunnen we uitgaan van een rechthoek ABDC (zie figuur a).
Identificeren we A met C en B met D dan krijgen we een ring.
Identificeren we daarentegen A met D en B met C dan krijgen we een M�bius-band (zie figuur b).

figuur c
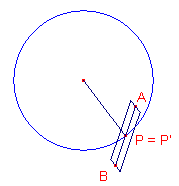
moebius3.gif (1903 bytes)

Uit de bovenstaande manier van defini�ren volgt, dat de doorsnede van de M�bius-band met een vlak door het middelpunt van de cirkel (bepaald door P en P'; zie figuur a) en een punt van de "defini�rende" cirkel, steeds een lijnstuk is met lengte AB.
Geven we de papierstrook een zekere dikte, dan kan de M�bius-band (nu wiskundig gezien een lichaam) worden voortgebracht als de meetkundige plaats van een rechthoekje waarvan het middelpunt P op de cirkel ligt en dat, na ��n doorloop over de cirkel, 180� gedraaid is (zie figuur c).

figuur d

Op deze manier is de Rhino-afbeelding (gerenderd met Flamingo) in figuur d ontstaan.

Klik hier voor een met Bryce5 gerenderde Rhino-afbeelding.
Klik hier voor een implementatie van de M�bius-band in Maple V (met VRML-plaatje).
Klik hier voor een met Bryce5 gerenderde afbeelding van het oppervlak.

[moebius.htm] laatste wijziging op: 27-12-04