Uitgaande van een rechthoek waarvan de zijden de lengte a en 1 hebben kunnen we door "herhaald aanpassen" van de lengtes van die zijden benaderingen van vierkantswortels vinden.
Benaderen van vierkantswortels
Meetkunde | Formule | Algemeen | Andere methodes ][ Rekenen
1. Meetkunde ![]()
Uitgaande van een rechthoek waarvan de zijden de lengte a en 1 hebben kunnen we
door "herhaald aanpassen" van de lengtes van die zijden benaderingen van
vierkantswortels vinden.
Voorbeeld
| zijde-1 (a) | zijde-2 (b) | gemiddelde van zijde-1 en zijde-2 | decimaal | |
| 1 | 5 | 1 | (5+1) / 2 = 3 | 3,00000 |
| 2 | 3 | 5/3 | (3 + 5/3) / 2 = 7/3 | 2,33333 |
| 3 | 7/3 | 5 / (7/3) | (7/3 + 15/7) /2 = 74/21 | 2,23810 |
| 4 | 94/42 | 5 / (94/42) | (94/42 + 210/94) / 2 = 2207/987 | 2,23607 |
| 5 | 2207/987 | 5 / (2207/987) | (2207/987 + 4935/2207) / 2 = 4870847/2178309 | 2,23607 |
In deze tabel is zijde-2 (b) telkens zo "aangepast" aan zijde-1 (a),
dat de oppervlakte van de rechthoek gelijk is aan 5 (ab = 5).
De aanpassing van de rechthoek vindt plaats door van de zijden a en b
het gemiddelde te nemen (zie 3e kolom)
De 4e kolom geeft de decimale vorm van de breuk in de 3e kolom.
Na een bepaald aantal herhalingen (zie rij 5) verandert de waarde in de 4e kolom niet
meer.
We hebben dan dus: (2,23607)2 � 5.
| figuur 1 | 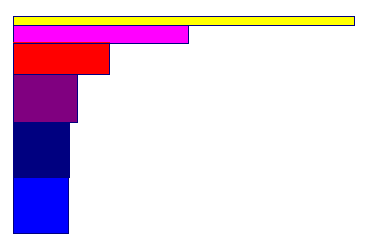 |
In nevenstaande figuur is een dergelijk proc�d� (men noemt het ook wel
een iteratieproces) in beeld gebracht. Begonnen is met de bovenste rechthoek. Alle rechthoeken hebben dezelfde oppervlakte. De onderste rechthoek is (bijna) een vierkant. |
In een recursieve betrekking wordt een element (a n+1) uit een rij getallen uitgedrukt in ��n of meer getallen uit die rij die aan dat element voorafgaan (in dit geval is dat alleen a n).
De rij getallen
3; 2,33333; 2,23810; 2,23607; …
geeft nu een steeds nauwkeuriger benadering van �5.
x n+1 = (x n + a / x n) / 2
bepaalt de rij x0, x1, x2, x3, …, x n, x n+1, … , die � a benadert.
4. Andere methodes
![]()
Er zijn natuurlijk ook andere methodes dan de methode die hierboven (in
paragraaf 1 ev.) is vermeld
We behandelen
4.1. methode met interpolatie
4.2. methode met behulp van de afgeleide
4.1. Interpolatie ![]()
Weten we (bijvoorbeeld gehele) getallen waartussen de vierkantswortel van
een getal gelegen is, dan kunnen we de waarde van de vierkantswortel gemakkelijk benaderen
door lineaire interpolatie.
Uitgaande van de grafiek van de functie f(x) = � x zien we (in figuur 2):
| figuur 2 | 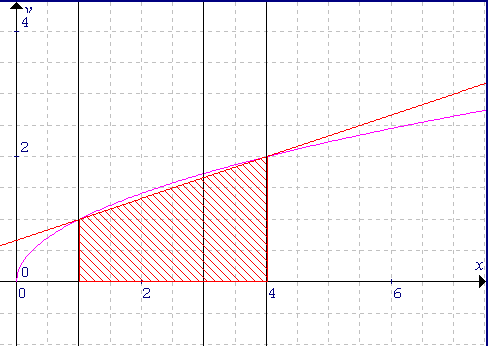 |
Willen we (bijvoorbeeld) � 3 berekenen,
dan weten we � 1 < � 3
< � 4. Dus 1 < � 3 < 2. Voor � 3 vinden we dan � 3 = 1 + (3-1)/(4-1) � (2-1) = 1 + 2/3 = 1,666... Nb. |
Algemeen
Weten we
q1 < � a
< q2, met q1 = � p1 en q2
= � p2
dan is (benaderd)
� a = (a-p1)/(p2-p1) � (q2 - q1)
4.2. Afgeleide ![]()
Voor een (differentieerbare) functie y = f(x) geldt voor
elke x (en voor kleine h, maar wat is 'klein' in dit geval?):
f '(x) = D y
/ D x = D y / h
of
D y = h �
f '(x)
en dus
f (x+h) = f (x) + h �
f '(x)
Hebben we nu: x = p, waarbij q = � p
(met bijvoorbeeld p zo, dat q geheel is), dan is dus
voor y = � x
met y ' = 1/(2� x):
� (p + h) = � p + h � 1/(2� p)
Voorbeeld
� 85 = � (81+4) = 9 + 4 � 1/(2 � 9)
= 9 + 2/9 = 9,222... (en beter benaderd: �85 = 9,2195...).
[vierkwort.htm] laatste wijzigingen op: 18-07-11