Een maximaliseringsprobleem
Probleem | Oplossing | Applet
][ Analyse
Probleem - De inhoud van een doosje 
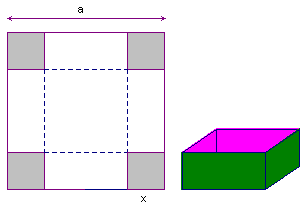
Van een vierkant met zijde a wordt aan elk hoekpunt eenzelfde kleiner vierkant
afgesneden (zie figuur 1).
De lengte van de zijde van zo'n kleiner vierkant is x.
Van het overblijvende deel ontstaat door vouwen een doosje in de vorm van een balk (recht
blok).
Voor welke waarde van x is de inhoud van de balk maximaal?
| figuur 1 |
 |
|
Oplossing 
We beschouwen de functie f die voor elke x de inhoud van de balk
bepaalt.
De lengte van de zijde van het grondvlak is: a - 2x.
De inhoud I van de balk is dan: I = x � (a -
2x)2, zodat
f(x) = x(a - 2x)2
Het domein van de functie is [0; �a].
Voor de afgeleide functie f ' van f hebben we (met de
productregel):
| f '(x) = |
1 � (a - 2x)2
+ x � 2(a - 2x) � (-2)
= |
|
(a - 2x)(a - 2x - 4x)
= |
|
2(a - 2x)(a - 6x) |
Het tekenschema van f ' is
| f '(x) |
+ |
++++++ |
0 |
---------- |
0 |
| x |
0 |
|
1/6a |
|
1/2a |
We zien, dat voor x = 1/6a een maximum
wordt bereikt.
Dit maximum is gelijk aan: f (1/6a)
= 1/6a (a - 1/3a)2
= 1/6a 4/9a2
= 2/27a3.
Applet 
Voor (bijvoorbeeld) a = 3,6 vinden we Imax = 2/27(3,6)3
= 3,456.
| figuur 2 |
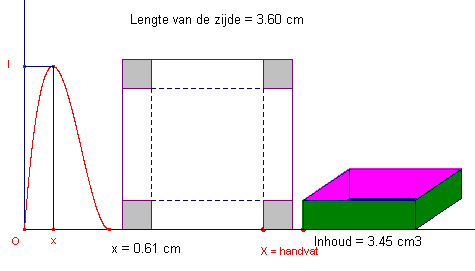 |
Figuur 2 is gegenereerd door een CabriJava applet.
Links in de figuur staat de grafiek van de hierboven beschreven functie f
met f(x) = I.Klik hier  voor het uitvoeren van deze
applet. voor het uitvoeren van deze
applet. |

[maxdoos.htm] laatste wijziging op: 12-02-01

