> local w0, w1, w2, a, y, x;
> a:=fl(labda, xstart, N);
> y:=labda*x*(1-x);
> w0:=plot( [a[1]], style=POINT, symbol=BOX );
> w1:=plot( [a], color=BLUE);
> w2:=plot( {y,x}, x=0..1, color=BLACK );
> display(w0,w1,w2);
> end:
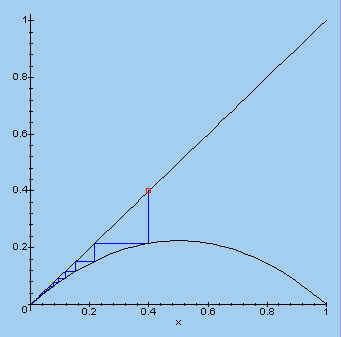
> plotset(0.9, 0.4, 30);
Iteratie | Fase-diagram | Iteratie-functies | Bifurcatie ][ De logistische functie (1) ][ DK & Maple
Een beschrijving van de logistische functie (VERVOLG)
met gebruikmaking van het computerprogramma Maple V, release 4
maart 1998
(Literatuur: Chaos, CWI-syllabus 1997)
1. Iteratie, anders bekeken
We geven nu een iets andere definitie van de procedure f1 (die behandeld is in deel 1). We genereren nu een lijst van geordende paren (xn,
xn), (xn, yn), waarbij
xn+1 = yn = l xn (1-xn)
De lijst bestaat dus telkens uit tweetallen.
> restart: with(plots):
> fl := proc(labda, xstart, N)
> local A, k, x,y, S;
> A:=array[1..2*N];
> A[1]:=[xstart,xstart];
> for k from 2 by 2 to 2*N do
> x:=A[k-1][2];
> y:=evalf(labda*x*(1-x),4);
> A[k]:=[x,y]; A[k+1]:=[y,y];
> od;
> S:=seq( A[k], k=1..2*N) ;
> end:
Voorbeeld
Met startwaarde x0 = 0.2 en l = 3,56 vinden we:
> fl(3.56, 0.2, 10);
[.2, .2], [.2, .5696], [.5696, .5696], [.5696, .8729], [.8729, .8729], [.8729, .3950], /
[.3950, .3950], [.3950, .8506], /[.8506, .8506],[.8506, .4524], [.4524, .4524], /
[.4524, .8822], [.8822, .8822], [.8822, .3700], [.3700, .3700], [.3700, .8297], /
[.8297, .8297], [.8297, .5031], [.5031, .5031], [.5031, .8899]
2. Fase-diagram
De procedure "plotset" gebruikt de logistische functie samen met het zogenoemde fase-diagram.
Het proces begint in het punt dat in de figuren aangegeven wordt door een vierkantje.
| > plotset :=
proc(labda, xstart, N) > local w0, w1, w2, a, y, x; > a:=fl(labda, xstart, N); > y:=labda*x*(1-x); > w0:=plot( [a[1]], style=POINT, symbol=BOX ); > w1:=plot( [a], color=BLUE); > w2:=plot( {y,x}, x=0..1, color=BLACK ); > display(w0,w1,w2); > end: > plotset(0.9, 0.4, 30); |
 |
We kiezen verder nog enkele andere waarden voor l en x0.
| > plotset(2.9, 0.2, 30); | 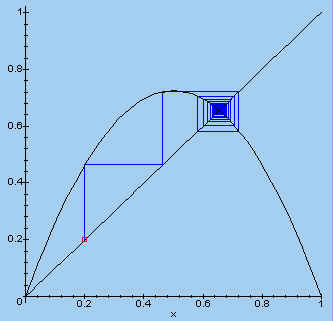 |
|
| > plotset(3.03, 0.9, 30); | 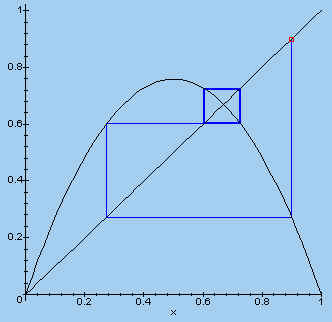 |
|
| > plotset(3.5, 0.123, 30); | 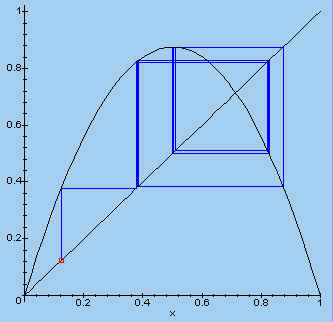 |
|
| > plotset(3.564, 0.5301, 30); | 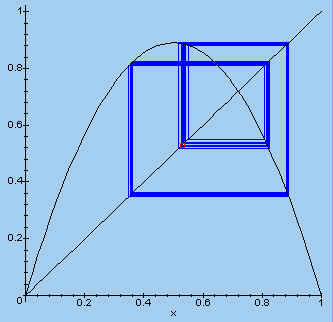 |
|
| > plotset(3.835, 0.123, 30); | 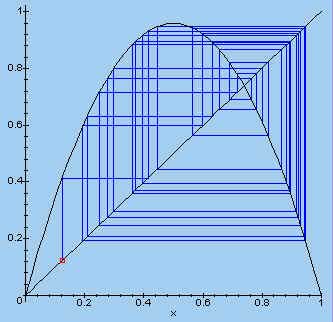 |
|
| > plotset(3.7386, 0.123, 100); | 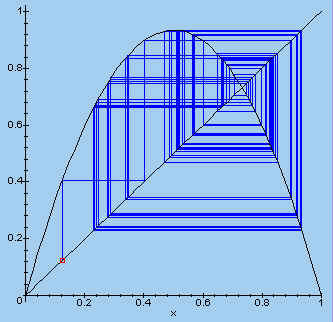 |
|
| > plotset(4, 0.123, 100); | 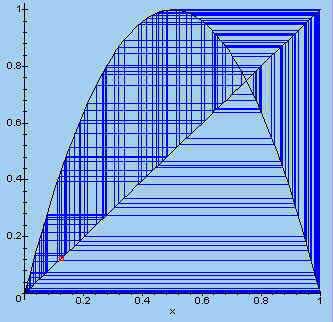 |
3. De iteratie-functies
We bekijken opnieuw de logistische functie f, gedefinieerd op het interval [0 ; 1], en met
a (was lamba) in ]0 ; 4].
> a:='a':
> f:=x->a*x*(1-x);
f := x -> a x (1 - x)
Iteraties van f op de uitkomstenverzameling van f schrijven we als f
= f1, f2, f3, ... waarbij
fn (x) = f ( f ( f ( f ... (x) ) )
)
of
fn (x)= (fn-1)(f (x) )
In Maple geeft dat:
> f1:=x->f(x);
> f2:=x->f(f1(x));
f1 := f
f2 := x -> f(f1(x))
> f3:=x->f(f2(x));
f3 := x -> f(f2(x))
> f4:=x->f(f3(x));
f4 := x -> f(f3(x))
Bovenstaande functies kunnen nu worden geevalueerd met het commando value.
> y2:=( value(f2(x)) );
> y3:=( value(f3(x)) );
> y4:=( value(f4(x)) );
y2 := a2 x (1 - x) (1 - a x (1 - x))
y3 := a3 x (1 - x) (1 - a x (1 - x))(1 - a2 x (1 - x) (1 - a x (1 - x)))
y4 := a4 x (1 - x) (1 - a x (1 - x))(1 - a2 x (1 - x) (1 - a x (1 - x))) /
(1 - a3 x (1 - x)(1 - a x (1 - x)) (1 - a2 x (1 - x) (1 - a x (1 - x))))
De geitereerde functies hebben zeer complexe functievoorschriften.
Het tekenen van zo'n functie is echter, via Maple, bijzonder eenvoudig.
| > a:=2.5: > plot( {x,f1(x),f2(x),f3(x)}, x=0..1 ); |
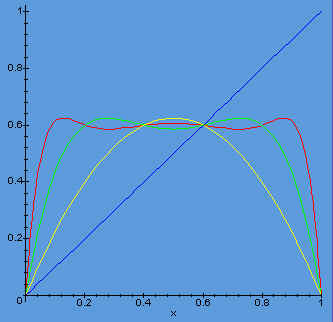 |
Om de evenwichtspunten (invariante punten) te vinden lossen we voor een willekeurige
waarde van a de volgende vergelijking op:
f1 (x) = x
> a:='a':
> S:=[solve(f1(x)=x ,x)];
![]()
De tweede oplossing (ongelijk aan 0) is interessant. Het is het niet-triviale evenwichtspunt
van de iteratie.
> lx:=S[2];
lx := (a-1)/a
> expand(lx);
1 - 1/a
In dit verband kijken we nog eens naar de functie met a = 2.5 en x0 = 0.05.
| > plotset(2.5, 0.05, 30); | 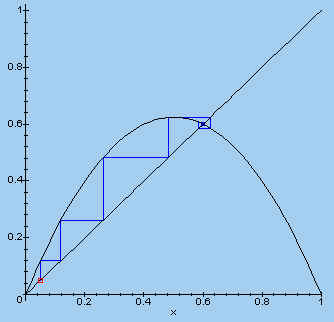 |
We zien, dat deze iteratie convergeert naar
> subs(a=2.5, lx);
.6000000000
Deze convergentie hangt samen met de afgeleide van f voor x = lx. Immers we
hebben
fa(lx) = lx
We kunnen nu afleiden
xn+1 - lx = fa(xn) - fa(lx)
Voor waarden van xn die weinig verschillen van lx, geldt op basis van de
afgeleide van f
fa' ( lx ) ? (fa(xn)
- fa(lx)) / (xn - lx)
Zodat voor de waarden van xn+1 (en dus ook voor de waarden van xn)
in een omgeving van lx geldt
xn+1 - lx ? fa'
(lx) (xn - lx)
Als nu de afgeleide van f in het evenwichtspunt in absolute waarde kleiner is dan
1, dan liggen opvolgende waarden van xn steeds dichter bij dat evenwichtspunt.
We berekenen de afgeleide f1acc van f voor a = 2.5 (hierboven
is lx gevonden als tweede oplossing in de verzameling S).
> a:=2.5:
> lx:=S[2];
> f1acc:=x->D(f)(x);
lx := .6000000000
f1acc := x -> a (1 - x) - a x
De waarde van de afgeleide in x = lx is dus gelijk aan:
> f1acc(lx);
-.500000000
In het bovenstaande geval zien we dus, dat als xn voldoende dicht bij lx
ligt, dan ligt xn+1 ongeveer 2 maal zodicht bij lx als xn, zodat de
rij {xn} snel naar lx convergeert.
Ten einde de convergentie voor gekozen a gemakkelijk te kunnen bestuderen,
berekenen we de waarde van de eerste afgeleide in het evenwichtspunt x = lx voor
willekeurige waarde van a.
> a:='a':
> lx:=S[2]: f1acc:=x->D(f)(x):
> f1acc(lx);
a(1 - (a-1)/a) - a + 1
> simplify(");
2 - a
> solve(abs(")<1, a);
RealRange(Open(1), Open(3))
Voor re?le waarden van a uit het (open) interval ]1 ; 3[ vindt dus
convergentie plaats naar het punt lx = 1 - 1/a.
Voor waarden van a uit ]0 ;1] vindt er convergentie plaats naar x = 0.
Dit kan blijken uit de afgeleide van f voor x = 0, maar ook uit de grafieken van fa
en y = x.
In dit laatste geval is er slechts ??n snijpunt van de rechte lijn en de grafiek van f,
namelijk x = 0.
In dit snijpunt is de afgeleide gelijk aan
> f1acc(0);
a
Voor waarden van a in het interval ]0 ; 1[ is er dus steeds convergentie naar 0, omdat de lijn y = x boven de grafiek van de logistische functie ligt.
| > plotset(0.9, 0.6, 10); | 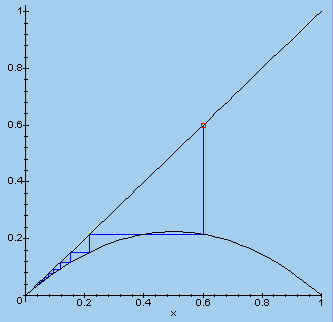 |
4. Het bifurcatiediagram
Wat er gebeurt als a in het interval [3 ; 4] is op het eerste gezicht niet
duidelijk.
We kunnen een en andere echter wel illustreren.
De iteratierij xn+1 = axn(1 - xn) hangt behalve
van a natuurlijk ook af van de startwaarde x0. Die afhankelijkheid van
x0 is echter in veel gevallen (zo niet in alle) een voorbijgaand verschijnsel:
op den duur dooft de invloed ervan uit.
De waarde van xn gaat dan, afhankelijk van de waarde van a, of naar
een evenwichtswaarde, of zich periodiek herhalen, of ze blijft chaotisch fluctueren.
Via een zogenoemd bifurcatiediagram kunnen we hiervan een globaal inzicht krijgen.
Op de horizontale as is de waarde van a in het interval [2.8 ; 4] uitgezet. Voor opvolgende waarden van a, met stappen ter grootte van 0,01 zijn telkens 300 waarden van een iteratie uitgevoerd uitgaande van een min of meer willekeurige waarde van x0. De eerste 200 stappen zijn opgevat als een 'inschakelverschijnsel': we gaan ervan uit dat de invloed van x0 daarna niet meer merkbaar is. De uitkomsten van de laatste 100 stappen worden daarna op de verticale as uitgezet.
We defini?ren eerst de procedure die de opvolgende iteratiewaarden in een rij zet en vervolgens tekent. Overigens, de reeks met punten wordt ook wel de Feigenbaum-reeks (Mitchell Feigenbaum, 1945 - ) genoemd.
> bifur := proc(begn,eind,stap)
> local k, x, a, s;
> s:={};
> a:=begn;
> while a<=eind do
> x:=0.1;
> for k to 200 do
> x:=a*x*(1-x)
> od;
> for k to 100 do
> x:=a*x*(1-x);
> s:=s union { [a,evalf(x,4)] };
> od;
> a:= a+ stap;
> od;
> plot( [ op (s)], 'a'=begn.. eind, style=POINT, symbol=POINT);
> end:
In onderstaande figuur zien we duidelijk, dat er op het interval [2.8 ; 3] convergentie
naar ??n waarde (namelijk 1 - 1/a) plaats vindt.
Vervolgens zien we stabiele punten met periode 2, 4, 8, enz. op het interval [3, 4].
| > bifur(2.8, 4, 0.01); | 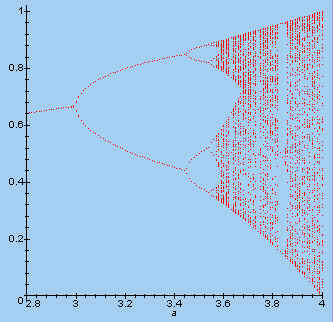 |
Uit het bifurcatiediagram blijkt dat het aantal stabiele punten voor een waarde van a
groter dan 3 gelijk is aan 2 en vervolgens bij een waarde van a iets groter dan
3,4 opnieuw verdubbelt.
Het ligt voor de hand deze waarden te onderzoeken door te kijken naar de oplossingen van
de vergelijking
f2 (x) = x
voor verschillende waarden van a..
> a:='a':
> S2:=[solve( f2(x) = x, x)];
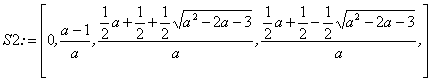
De beide eerste oplossingen van S2 vonden we reeds uit f1(x) = x.
De beide andere oplossingen zijn verschillend, als
a2 - 2a - 3 > 0
> solve(a^2-2*a-3 > 0, a);
RealRange(-infinity, Open(-1)), RealRange(Open(3), infinity)
Uit het bovenstaande blijkt dus, dat er twee takken zijn op het interval ] 3, ? [, immers we bekijken geen negatieve waarden van a.
De eerste verdubbeling vinden we dus bij a = 3.
Het ligt voor de hand verdere bifurcaties te onderzoeken met de vergelijking
f3 (x) = x
Dit leidt echter tot een 8e graads vergelijking, die ook Maple niet aan kan.
> S3 := [ solve( f3(x) = x, x) ];
S3 := [0, (a - 1) / a, RootOf(a2 + a + 1 + (-1 - 2a2 - 2a - a3 ) _Z +
+ (3a + 1 + 2a3 + 3a2 ) _Z2 + (-3a - 1 - 5a2 - a3 ) _Z3 +
+(4a + 3a2 + 1) _Z4 + (-1 - 3 a) _Z5 + _Z6 ) / a]
De tweede bifurcatie
We benaderen het probleem voor het vinden van de waarde van a bij de tweede bifurcatie
daarom op een iets andere manier.
We kiezen x3 en x4 als beide niet-triviale oplossingen van S2:
> x3 := S2[3]; x4 := S2[4];
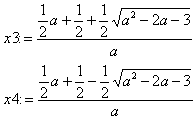
Deze oplossing zijn wortels van een vierkantsvergelijking die we kunnen vinden door de
vergelijking
f2 (x) - x = 0
te delen door opvolgend x (immers x = 0 is oplossing van die vergelijking) en x - 1 + 1/a
(immers x = 1 - 1/a is ook een oplossing).
> verg := f2(x) - x = 0;
verg := a2 x (1 - x) (1 - a x (1 - x)) - x = 0
> verg:=simplify(verg/x);
> verg:=simplify(verg/(x-1+1/a));
verg := a2 - a x +
2 a3 x2 - a2 x - a3 x3 - 1 = 0
verg := -(a2 x2 - a2 x + a - a x + 1) a = 0
Omdat a ongelijk is aan 0, kunnen we ook nog delen door -a:
> verg:=simplify(verg/(-a));
verg := a2 x2 - a2 x + a - a x + 1 = 0
Deze vergelijking heeft natuurlijk de genoemde waarden x3 en x4 als wortels, hetgeen ook na substitutie van beide waarden blijkt.
> collect(verg,x);
a2 x2 + (-a2 - a) x + a + 1 = 0
> linkerlid := lhs(");
linkerlid := a2 x2 + (-a2 - a) x + a + 1
> simplify( subs(x=x3, linkerlid) );
> simplify( subs(x=x4, linkerlid) );
0
0
In het linkerlid van deze kwadratische vergelijking zien we nu eenvoudig de waarden
voor x3 + x4 (sum_w) en x3*x4 (prd_w).
Deze waarden kunnen we natuurlijk ook direct berekenen uit de gevonden toekenningen aan x3
en x4. Voor het berekenen van het product van de wortels is het commando expand
nodig, om daadwerkelijk de vermeningvuldiging te kunnen uitvoeren.
> sum_w:=simplify(x3+x4);
> prd_w:=simplify(expand(x3*x4));
sum_w := (a+1) / a
prd_w := (a+1) / a2
We kijken nu naar de afgeleide f2' (geschreven als f2acc) van f2.
> f2acc := diff(f2(x),x);
f2acc := a2 (1 - x) (1 - a x (1 - x)) - a2 x (1 - a x (1 - x)) + a2 x (1 - x) (-a (1 - x) + a x)
> f2acc_x3:=subs(x=x3, f2acc):
> f2acc_x3:=simplify(");
f2acc_x3 := -a2 + 2 a + 4
> f2acc_x4:=subs(x=x4, f2acc):
> f2acc_x4:=simplify(");
f2acc_x4 := -a2 + 2 a + 4
Wat we zien is, dat deze beide afgeleiden gelijk zijn. Dit is geen toeval. We kunnen
dit met eenvoudige differentiaalrekening bewijzen.
We weten dat f(x3) = x4 en verder ook dat f2(x3)
= x3 (zie hiervoor de definitie van x3 als oplossing van de
vergelijking f2(x) = x, en dus f(f(x3)) =
f(x4) = x3.
Verder is volgens de kettingregel van de differentiaalrekening:
f2acc(x) = d/dx( f2(x) ) = d/dx(
f(f(x)) )= f '(f(x)) f '(x).
Bekijken we deze afgeleide voor x = x3, dan zien we dat
f2'(x3) = f '(f(x3))
f '(x3) = f '(x4) f '(x4)
Vanwege de volledige symmetrie is dus ook:
f2'(x4) = f '(f(x4))
f '(x4) = f '(x4) f '(x4)
We kijken nu voor welke waarden van a geldt dat
f2'(x3) = -1
> S3 := [ solve( f2acc_x3 = -1, a) ];
S3 := [1 + ?6 , 1 - ?6 ]
De waarde waarvoor de tweede bifurcatie optreedt is dus
> S3[1];
1 + ?6
In decimalen is dat :
> evalf(", 4);
3.449
Voor deze waarde van a tekenen we nog eens het stappendiagram, waaruit de 4
stabiele punten duidelijk blijken.
| > plotset(S3[1], 0.1, 100); | 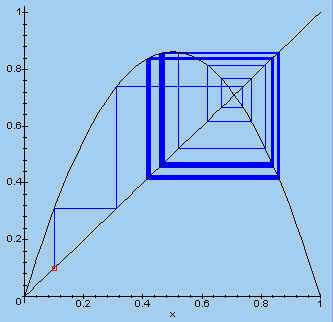 |
[ De logistische functie (1) ] [ DK & Maple ]
[logistic2.htm] laatste wijziging op: 23-02-2001