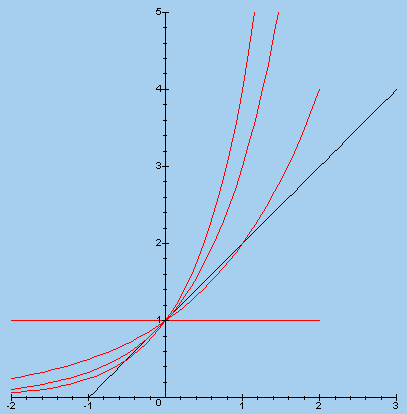 |
f(x) = ax
voor a=1,2,3,4 g(x) = 1 + x |
De functie ax |
Benaderingen | Raking | De
functie ex | Richtingsco?ffici?nt | Gebruik van (ax)'
[ DK & Analyse | DK & Maple ]
De waarde van e,
het getal van Euler - een worksheet in Maple V, release 4
maart 1998
1. De
exponti?le functie f(x) = ax
We bekijken eerst de grafiek van de functie f(x) = ax
voor verschillende waarden van a.
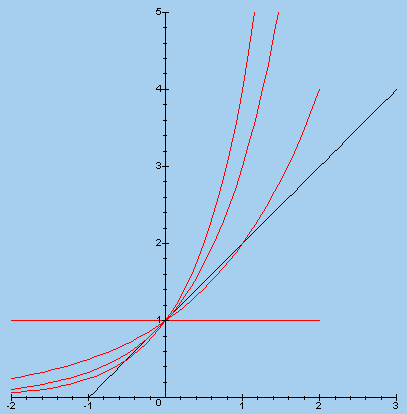 |
f(x) = ax
voor a=1,2,3,4 g(x) = 1 + x |
Daarnaast beschouwen we telkens de grafiek van de functie g(x) = 1 + x.
Allereerst berekenen we de waarde van a indien de
beide grafieken elkaar snijden in de punten (0,0) en (1,2).
Omdat de beide grafieken elkaar voor elke waarde van a
in het punt (0,0) snijden, moeten we oplossen de vergelijking:
ax = 1 + x
voor x=1.
Dit geeft onmiddellijk a = 2.
De grafieken van 2x en 1 + x
kunnen natuurlijk in dezelfde figuur worden getekend.
> restart;
> plot({2^x,1+x},x=-2..2);
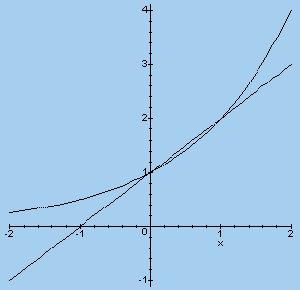 |
f(x)
= 2x |
2.
Benaderingen
Snijding voor x=1/2
We trachten vervolgens de waarde van a te bepalen
waarvoor de beide grafieken elkaar, naast (0,0), snijden in
(1/2,1+1/2).
Daartoe dienen we de vergelijking
a? = 1 + ?
op te lossen.
Dit kan nog (net) met de hand, door beide kanten van de
vergelijking te kwadrateren. Dit geeft
a = (1 + ?)2 of a = 9/4.
Maar we kunnen natuurlijk ook gebruik maken van Maple zelf.
> fsolve(a^(1/2)=1+1/2,{a});assign(");
{a = 2.250000000}
> plot({2^x,a^x,1+x}, x=-2..2,y=-1..3);
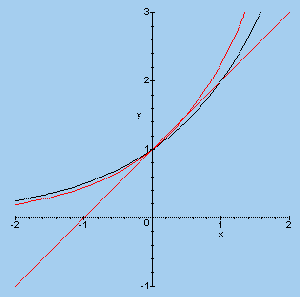 |
f1(x) = 2x f2(x) = 2.25x g(x) = 1 + x |
Snijding voor x=1/4
Vervolgens berekenen we de waarde van a als de grafieken
elkaar snijden in het punt (1/4, 1+1/4).
> a:='a':
> fsolve(a^(1/4)=1+1/4,{a}); assign(");{a = 2.441406250}
Snijding voor x=1/10
Tenslotte wordt de waarde van a berekend als de
grafieken elkaar snijden in het punt met x = 1/10.
> a:='a':
> fsolve(a^(1/10)=1+1/10,{a});assign(");{a = 2.593742460}
3. Op weg
naar raking in het punt (0,1)
We proberen nu het tweede snijpunt in de buurt van het punt (0,
1) te brengen, waardoor we de waarde van a kunnen vinden
waarvoor de grafieken van ax en
1 + x in het punt (0, 1) aan elkaar raken.
We laten nu Maple de waarde van a berekenen voor x = 0.01.
> a:='a':
> fsolve(a^(1/100)=1+1/100, {a}): assign(");
> evalf(a);2.704813829
Limiet voor x naderend naar 0
Uit ax = 1 + x
volgt algemeen a = (1 + x)1/x.
We berekenen nu met Maple de waarde van a als x
nadert tot 0; dus (in Maple-notatie):
limit((1 + x)^(1/x), x = 0)
De uitkomst van deze limiet is het getal e, het getal van Euler.
> Limit((1+x)^(1/x),x=0):"=value(");
lim (1 + x)1/x = e x -> 0
De exponenti?le functie met dit grondtal, ex, wordt in Maple aangegeven met exp(x). De waarde van het getal e kunnen we dus (we doen het in 14 decimalen) berekenen met
> evalf(exp(1),15);
2.71828182845905
Opmerking
Indien de serie getallen 1/x in bovenstaande limiet
wordt vervangen door n, dan krijgen we (ook weer in
Maple-notatie)
limit((1+(1/n))^n, n= infinity)
Deze limiet kunnen we natuurlijk ook met Maple berekenen:
> Limit((1+1/n)^n,n=infinity): "=value(");
lim (1 + 1/n)n = e n -> ?
4. De
grafiek van ex
In onderstaande figuur zien we nu de grafiek van de exponentiele
functie ex en van 1 + x.
> plot({exp(x),1+x}, x = -2..2);
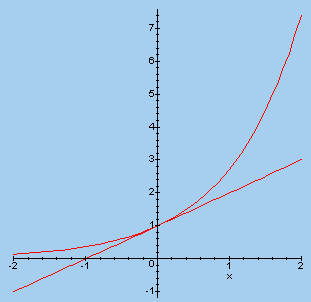 |
f(x) = ex g(x) = 1 + x |
We vergroten de zaak nog eens uit voor waarden van x dicht in
de buurt van 0. We zien dan dat de grafieken elkaar dan
nauwelijks ontlopen.
De grafiek van 1 + x is 'dus' de raaklijn aan
de grafiek van ex.
> plot({exp(x),1+x}, x = -0.1..0.1);
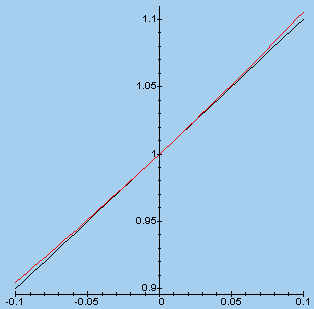 |
f(x) = ex g(x) = 1 + x |
5. De
richtingscoefficient aan de grafiek van ax in
x = 0
We nemen allereerst a = 2.
Zoals bekend is uit de differentiaalrekening kunnen we de
afgeleide van ax in x = 0,
de richtingsco?ffici?nt, benaderen via het differentiequotient.
Daartoe nemen voor h een kleine waarde, zeg h = 0.0001,
en berekenen de uitkomst van
(2h-1) / h
> h:=0.0001:
> deltay:=(2^h-1)/h;deltay := .6931700000
We nemen vervolgens a = 3 en berekenen opnieuw het differentiequotient, bij dezelfde waarde van h:
> deltay:=(3^h-1)/h;
deltay := 1.098670000
We zullen nu de waarde van a zo bepalen dat deltay = 1,
opnieuw bij dezelfde waarde van h.
We moeten dus de vergelijking
(ah-1) / h = 1 of ah - 1 = h
oplossen. Dit kunnen we direct in Maple doen.
> a:='a':
> fsolve(a^h-1=h, {a}); assign(");
{a = 2.718145927}
We vergelijken deze waarde van a met de waarde van e.
> evalf(abs(a-exp(1)));
.000135901
We zien dat de waarde van enigzins afwijkt van de waarde van e. Dit wordt natuurlijk veroorzaakt door het gebruik van de benadering van het differentiaalquotient via het differentiequotient.
We kunnen dus stellen, dat de richtingscoefficient van de raaklijn aan de functie ex in x = 0 gelijk is aan 1.
6. Gebruik van de afgeleide van ax
In hetgeen volgt gebruiken we de definitie van afgeleide bij het
berekenen van de de richtingscoefficient in x = 0
aan de grafiek van ax.
Deze definitie luidt algemeen voor x = 0 (in
Maple-notatie):
diff(a^x ,x) = limit( (a^h-1) / h, h=0)
En dus:
> a:='a': h:='h':
> Limit((a^h-1)/h, h=0):"=value(");
ah - 1 lim ------ = ln(a) h -> 0 h
We zien dat de waarde van bovenstaande limiet door Maple wordt
weergegeven met ln(a).
Deze uitkomst kunnen we door middel van opeenvolgende
benaderingen aannemelijk maken (toelichten).
We kiezen daartoe opnieuw a = 2 en a = 3 en berekenen beide limieten:.
2h - 1 lim ------ = .6931471806 h -> 0 h |
> Limit((3^h-1)/h, h=0): "=evalf(");
3h - 1 lim ------ = 1.098612289 h -> 0 h |
We moeten nu het getal a zo bepalen, dat de uitkomst
van de limiet gelijk is aan 1.
Hieronder staan enkele van die benaderingen.
h 2.7 - 1 lim -------- = .9932517730 h -> 0 h |
> a:=2.8:
> Limit((a^h-1)/h, h=0): "=evalf(");
h 2.8 - 1 lim -------- = 1.029619417 h -> 0 h |
Nu is duidelijk dat de gezochte waarde van a tussen
2.7 en 2.8 moet liggen.
We benaderen dus opnieuw.
2.71h - 1 lim --------- = .9969486349 h -> 0 h |
> a:=2.72:
> Limit((a^h-1)/h, h=0): "=evalf(");
2.72h - 1 lim --------- = 1.000631880 h -> 0 h |
||
2.718h - 1 lim ---------- = .9998963157 h -> 0 h |
> a:=2.719:
> Limit((a^h-1)/h, h=0): "=evalf(");
2.719h - 1 lim ---------- = 1.000264166 h -> 0 h |
En tenslotte nog:
2.7182h - 1 lim ----------- = .9999698965 h -> 0 h |
> a:=2.7183:
> Limit((a^h-1)/h, h=0): "=evalf(");
2.7183h - 1 lim ----------- = 1.000006685 h -> 0 h |
We zien dus dat hiermee een redelijke benadering van het getal
e kan worden
verkregen.
Zoals we hierboven hebben gezien kunnen de uitkomsten van de
limiet worden opgevat als functiewaarden van de functie
y = ln(x).
Voor de laatste twee waarden van a berekenen we die functiewaarden direct:
> ln(2.7182); > ln(2.7183);
.9999698965 1.000006685
We hebben dus gevonden:
2.7182 < e < 2.7183
Tenslotte nog eens e in 40 decimalen:
> evalf(exp(1), 41);
2.7182818284590452353602874713526624977572
[expon.htm] laatste wijziging op: 24-04-1999