Joukowski-afbeelding

Overzicht  ][  Complexe afbeeldingen

0. Overzicht terug

  1. Inleiding cabrisignal.gif (160 bytes)
  2. Vleugelprofiel cabrisignal.gif (160 bytes)
  3. Andere vormen cabrisignal.gif (160 bytes)
  4. Herhaalde afbeelding cabrisignal.gif (160 bytes)
     
  5. Download
  6. Referenties

1. Inleiding terug

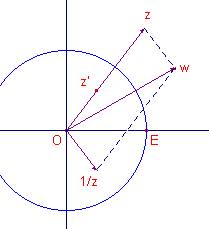jouk1.gif (3259 bytes) Voor een complex getal z heet de afbeelding
     w = z + 1/z
de Joukowski-transformatie van het complexe vlak.
w heet het Joukowski-beeld (J-beeld) van z.

 

Klik hier animatie voor een CabriJavapplet van de J-afbeelding.

Uit de applet blijkt (oa.):

2. Vleugelprofiel terug
Het J-beeld van een cirkel die door het punt z = -1 gaat,  heeft bij geschikte keuze een bijzondere vorm: het profiel van een vliegtuigvleugel.

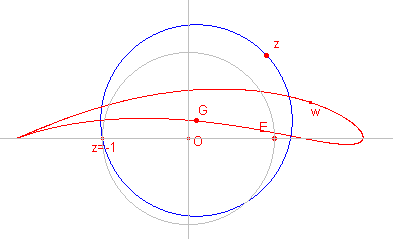jouk2.gif (4026 bytes) In de figuur hiernaast is G het middelpunt van de "basiscirkel". Het punt z ligt op cirkel G. w is het J-beeld van z.

Klik hier animatie voor een CabriJavapplet ter illustratie.

3. Andere vormen terug
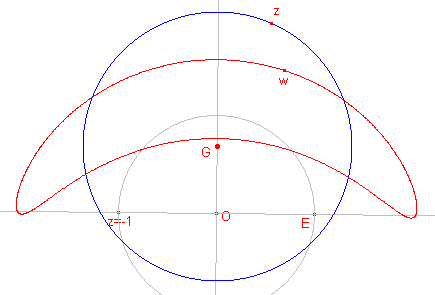
Hieronder staan enkele andere beeldfiguren van een cirkel.

jouk4.gif (4948 bytes)   





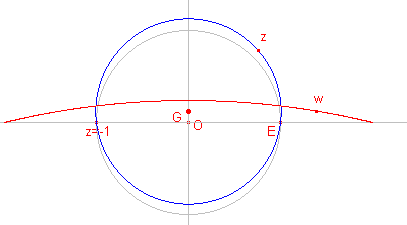jouk4b.gif (3755 bytes)
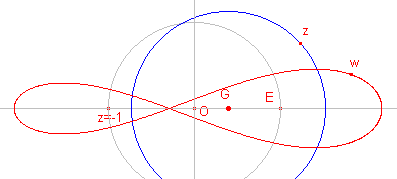
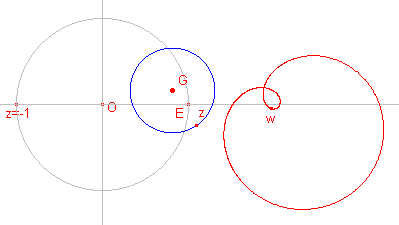
G op de y-as; E en z = -1 binnen de cirkel G op de y-as; cirkel door E

Klik hier animatie voor een CabriJavapplet ter illustratie.

jouk3.gif (3812 bytes) jouk3b.gif (3903 bytes)
G op de x-as; E binnen de cirkel, z = -1 buiten de cirkel G willekeurig; E binnen de cirkel

4. Herhaalde afbeelding terug

jouk5.gif (4749 bytes)

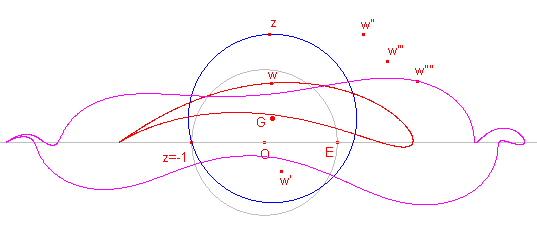
 Op het beeld w van z kunnen we natuurlijk ook de J-afbeelding toepassen.
Hiernaast is G het middelpunt van een cirkel door z = -1.
w is het J-beeld van z.
w' is het J-beeld van w.
jouk5b.gif (4674 bytes) Hiernaast is: w"" = J (5) (z)
De tussenliggende figuren zij niet alle getekend.
         jouk6.gif (2545 bytes) Herhaalde uitvoering van de Joukowski-afbeelding van een punt, zie ook de laatste figuur hierboven geeft, bij bepaalde ligging van z, aanleiding tot convergentie naar de assen.

Klik hier animatie voor een CabriJavapplet ter illustratie.
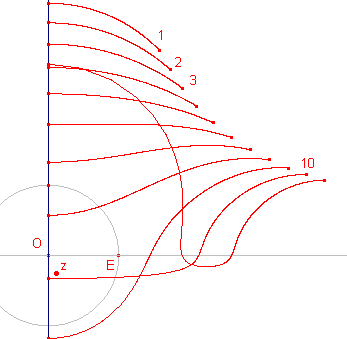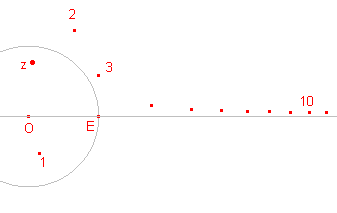
jouk7.gif (4625 bytes) Als z op de y-as ligt, liggen alle beeldpunten bij de herhaalde afbeelding eveneens op de y-as (zie paragraaf 1).
Laten we een punt z tot de y-as naderen, dan leggen de beeldpunten onverwachte wegen af.

Hiernaast zijn de herhaalde beelden getekend uitgaande van het punt z(0,12 ; -0,26) dat nadert tot (0 ; -0,26).

5. Download terug
Enkele figuren op deze webpagina, alsmede de figuren gebruikt in de CabriJavapplets, en de macro JoukowskiBeeld.mac kunnen in ��n bestand via deze website worden gedownload.
Klik hier om het download proces te starten (ZIP-bestand, ca. 8kB).

6. Referenties terug

[1] H. VAN LOOY, Joukowski-transformatie, in: Wiskunde & Onderwijs, nr 82 (p. 212, ev)
[2] J. OLIVE, Creating Airfoils from Circles: The Joukowski Transformation, in: Geometry Turned On!, MAA (1997)

begin pagina

[joukowski.htm] laatste wijziging op: 29-07-02